2021. 2. 4. 10:03ㆍ알고리즘/알고리즘 정리
1. 트리
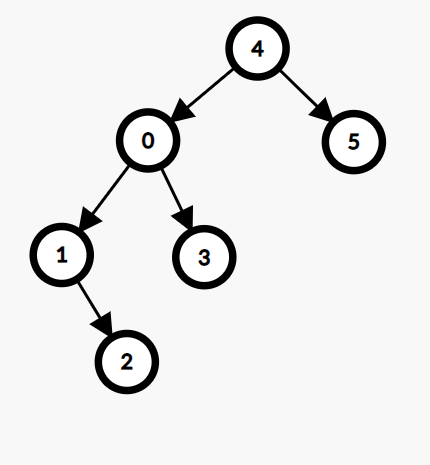
트리는 계층 관계를 갖는 객체들을 표현하기 위해 만들어진 자료 구조이다.
계층 관계표현 이외도 다른 구조보다 같은 연산을 더 빠르게 할 수 있다.
(특히 탐색형 자료 구조)
탐색형 트리 자료구조의 유명한 이진 검색 트리는
모든 숫자에 최대 두개의 하위 숫자만 있으며
어떤 숫자에서든 왼쪽 가지를 따라 내려가면 더 작은 수를
오른쪽 가지를 따라 내려가면 더 큰 수를 만날 수 있다.
이와 같은 특별한 규칙에 의해 탐색을 lgn만에 할 수 있게 된다.
트리의 구성 요소
노드 node: 연결된 노드 간에는 상하위 관계가 있다.
간선 edge: 연결하는 선
상위 노드 parent
하위 노드 child
부모가 같은 노드 sibling
부모 노드와 그의 부모 노드들 ancestor
자식 노드와 그의 자식 노드들 descendant
다른 모든 노드들을 자손으로 갖는 노드 root
자식이 하나도 없는 노드들 leaf
트리의 노드와 속성
루트에서 어떤 노드에 도달하기 위해 거쳐야 하는 간선의 수를 해당 노드의 깊이의 수 depth
트리에서 가장 깊숙히 있는 노드의 깊이 height
자손이 없을 경우 height = 0
트리의 재귀적 속성
트리가 유용하게 사용되는 이유 중 하나인 재귀적 성질, 이로인해 관련 함수들은 재귀 호출로 대개 구현된다.
트리에서 한 노드와 그의 자손들을 연결하면 '트리'가 된다.
어떤 노드 t와 그 자손들로 구성된 트리를 't를 루트로 하는 서브트리라고 한다 subtree
그러므로 모든 트리는 루트와 루트 밑에 있는 서브트리들의 집합이다.
트리의 표현
각 노드를 하나의 구조체/객체로 표현.
각 노드들을 서로의 포인터로 연결
각 노드들은 자신의 부모와 모든 자손들에 대한 포인터로 연결
struct TreeNode {
string label;
TreeNode* parent;
vector<TreeNode*> children;
};
노드 객체들은 특정 구조나 형태를 가정하지 않는다. 가장 기초적인 조건만 만족하면 된다.
그러나 트리의 구조나 사용 용도가 제한되어 있는 탐색용 트리에서는
효율성을 위해 좀 더 단순한 형태의 구현을 자주 사용한다.
(BST: 왼쪽 오른쪽에 최대 하나씩의 자식. 동적 배열대신 포인터 left, right 만 이용)
(heap: 배열을 사용해 표현 가능)
(상호 배타적 집합 구조: 각 노드가 자신의 부모를 가리키는 포인터만 가짐, 부모는 각 자식에 대해 정보가 없음)
2. 트리의 순회
트리의 재귀적 속성을 이용해야한다.
모든 트리는 각 자식들을 루트로 하는 서브트리와 루트로 나눌 수 있음.
따라서 루트가 주어지면 루트 방문 후 서브트리르 재귀적으로 방문하는 함수로 순회 가능.
void printLabels(TreeNode* root) {
cout<<root->label<<endl;
for(int i = 0; i < root->children.size(); i++)
printLabel(root->children[i]);
}
순회를 이용하여 높이 또한 계산할 수 있다.
int height(TreeNode* root){
int h = 0;
for(int i = 0; i < root->children.size(); i++)
h = max(h, 1 + height(root->children[i]));
return h;
}
전체 수행 회수는 n-1 이므로 O(n)의 시간이 걸린다.
이진 트리 순회에는 3가지 종류가 있다.
전위 순회 preorder : VLR 서브트리에서 루트를 먼저 출력하고 왼쪽->오른쪽 탐색
중위 순회 inorder : LVR 서브트리에서 왼쪽을 먼저 탐색하고 루트를 출력 -> 오른쪽탐색
후위 순회 postorder : LRV 서브트리에서 왼쪽->오른쪽 탐색하고 루트 출력.
구현은 다음과 같다
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
|
struct TreeNode {
int index;
TreeNode *mother;
TreeNode *left, *right;
TreeNode(int _index): index(_index){ left = nullptr; right = nullptr; mother = nullptr;}
};
void preOrder(TreeNode* root)
{
if(root == nullptr) return;
cout<<root->index<<" ";
preOrder(root->left);
preOrder(root->right);
}
void inOrder(TreeNode* root)
{
if(root == nullptr) return;
preOrder(root->left);
cout<<root->index<<" ";
preOrder(root->right);
}
void postOrder(TreeNode* root)
{
if(root == nullptr) return;
preOrder(root->left);
preOrder(root->right);
cout<<root->index<<" ";
}
|
cs |
트리에서 가장 긴 경로를 찾는 재귀 호출 알고리즘
트리에서의 가장 긴 경로는 두가지의 경우에서만 구할 수 있다.
1. 루트 -잎 경로 : 높이
2. 잎 - 잎 경로
잎-잎 경로는 항상 어떤 노드까지 올라갔다가 내려온다.
이 노드는 두 잎의 선조 노드이고 경로의 최상위 노드라고 부른다.
각 노드마다 각 노드를 최상위 노드로 갖는 가장 긴 잎-잎 경로를 계산하고 그중에 최댓값을 선택하는 것이다.
주어진 노드를 최상위 노드로 갖는 가장 긴 잎-잎 경로:
이 경로는 현재 노드의 자손 노드 중 한쪽에서 올라와서 다른 자손 노드로 내려갈 것이다.
이때 경로의 올라오는 부분과 내려가는 부분의 길이는
각각의 자손 노드를 루트로 하는 서브트리의 높이에 1을 더한 것이 된다.
따라서 가장 긴 서브 트리의 높이 두개와 2를 더하면 된다.
다음은 O(nlgn)의 시간이 걸리지만 정렬을 하지 않고
최댓값 두개만 찾으면되므로 O(n)으로 구현 할 수 도 있다.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
|
struct TreeNode {
vector<TreeNode*> children;
};
int longest;
int height(TreeNode* root)
{
vector<int> heights;
for(int i = 0 ; i < root->children.size(); i++)
heights.push_back(height(root->children[i]));
if(heights.empty()) return 0;
sort(heights.begin(), heights.end());
if(heights.size() >= 2)
longest = max(longest, 2 + heights[heights.size()-2] + heights[heights.size() - 1]);
return heights.back() + 1;
}
int solve(TreeNode* root)
{
longest = 0;
int h = height(root);
return max(longest, h);
}
|
cs |
- 알고리즘 문제해결전략 681p
'알고리즘 > 알고리즘 정리' 카테고리의 다른 글
| [트리] Tree 5: 우선순위 큐와 이진 힙 (0) | 2021.02.06 |
|---|---|
| [트리] Tree 2: 이진 검색 트리, 트립 (0) | 2021.02.04 |
| [문자열] kmp 알고리즘, 맨버-마이어스 알고리즘 (0) | 2021.01.31 |
| 큐와 스택 그리고 데크 (0) | 2021.01.29 |
| [선형 자료 구조] 동적 배열과 연결 리스트 (0) | 2021.01.29 |