2021. 2. 18. 20:58ㆍ알고리즘/알고리즘 정리
1. 최단 경로 문제 (shortest path problem) : 가중치 있는 그래프
최단 경로 문제란 주어진 그래프에서 주어진 두 정점을 연결하는 가장 짧은 경로의 길이를 찾는 문제로,
그래프의 응용 문제 가운데 가장 유용하고 널리 사용된다.
가중치가 없는 그래프에 대한 최단 경로는 BFS를 사용하면 되므로
여기서는 가중치 있는 그래프에 대한 알고리즘을 다룬다.
이 알고리즘들은 '최단 경로'를 구성하는 정점들의 목록을 구해주는 것이 아니라
'최단 경로의 길이'를 찾아 주는 것들이다.
실제 경로를 얻어내려면 탐색 과정에서 별도의 정보를 저장하고, 이것으로부터 실제 경로를 찾아내는 코드를 작성해야한다.
다양한 그래프의 종류와 특성에 따라 알고리즘의 효율성이 달라지기 때문에 많은 경로 알고리즘이 존재한다.
간선(u, v)의 가중치 = w(u,v)
2. 음수 간선의 중요성
음수 간선을 갖는 그래프는 가중치의 합이 음수인 사이클(음수 사이클)이 등장할 수 있다.
음수 사이클로 인해 경로의 길이는 음의 무한대 까지 가버리기 때문에 이런 그래프는 최단 경로를 정확하게 찾아줄 수 없으며,
알고리즘에 따라 음수 사이클의 존재 여부만 확인 할 수 있다.
3. 단일 시작점과 모든 쌍 알고리즘
이 장에서 다루는 최단 경로 알고리즘들은 크게 단일 시작점 알고리즘과
모든 쌍 알고리즘으로 나뉜다.
단일 시작점 알고리즘들은 너비 우선 탐색과 비슷하게, 하나의 시작점에서 다른 모든 정점까지 가는 최단 거리를 구해준다.
모든 쌍 알고리즘은 모든 정점의 쌍에 대해 최단 거리를 계산한다.
따라서 모든 쌍 알고리즘의 수행결과는 V*V크기의 배열이 된다.
이 배열의 각 원소는 두 정점 사이의 최단 거리를 나타낸다.
단일 시작점 알고리즘을 V번 수행해서 같은 일을 할 수 있지만,
플로이드의 최단 경로 알고리즘은 그 구현이 엄청 간단하고 효율적이기 때문에 이를 사용한다.
4. 방향 그래프와 무방향 그래프
여기서 다루는 그래프는 전부 방향 그래프이다.
무방향 그래프 위에서의 최단 경로를 찾기 위해서는 각각의 양 방향 간선을 두 개의 일방 통행 간선으로 쪼개서
방향 그래프로 만들어야한다.
그러나 음수 가중치가 있는 무방향 그래프는 두 개로 쪼개면 이 둘만으로 음수 사이클을 만들기 때문에
항상 최단 경로 문제를 제대로 풀 수 없다.
5. 다익스트라의 최단 경로 알고리즘(Dijkstra) : 음수 사이클이 없는 그래프, 그리디
다익스트라의 최단 경로 알고리즘은 가장 유명한 알고리즘 중 하나이다.
다익스트라는 단일 시작점 최단 경로 알고리즘으로
시작 정점 s에서부터 다른 정점들까지의 최단 거리를 계산한다.
우선순위 큐를 사용하는 너비 우선 탐색
다익스트라 알고리즘은 너비 우선 탐색과 유사한 형태를 가진 알고리즘으로,
너비 우선 탐색처럼 시작점에서 가까운 순서대로 정점을 방문해 나간다.
가중치가 있는 그래프에서는 너비 우선 탐색을 그대로 적용할 수 없다.
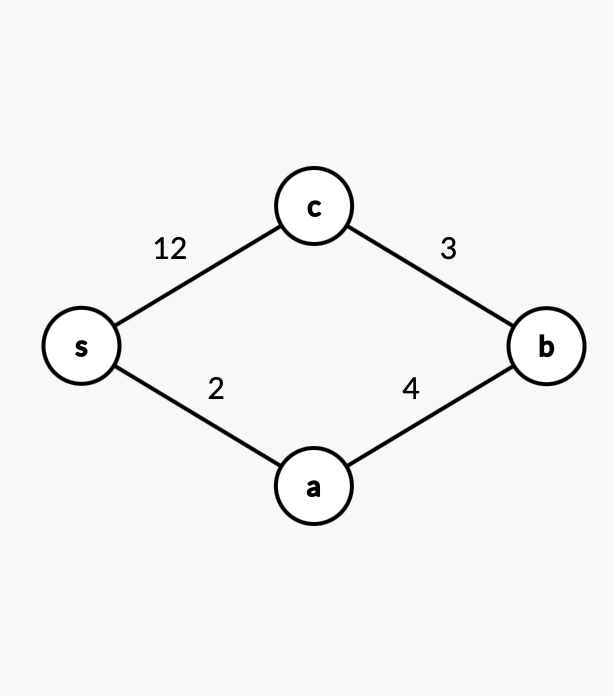
너비 우선 탐색은 각 정점을 발견한 순서대로 방문하기 때문에 a와 c를 방문한 후에야 b를 방문하게 된다.
하지만 s에서 c까지 가는 최단 경로는 s-a-b-c이기 때문에
최단 거리 순서대로 정점들을 방문하려면 a, b, c순서로 각 정점을 방문해야한다.
이것은 더 늦게 발견한 정점이라도 더 먼저 방문할 수 있어야 한다는 의미이다.
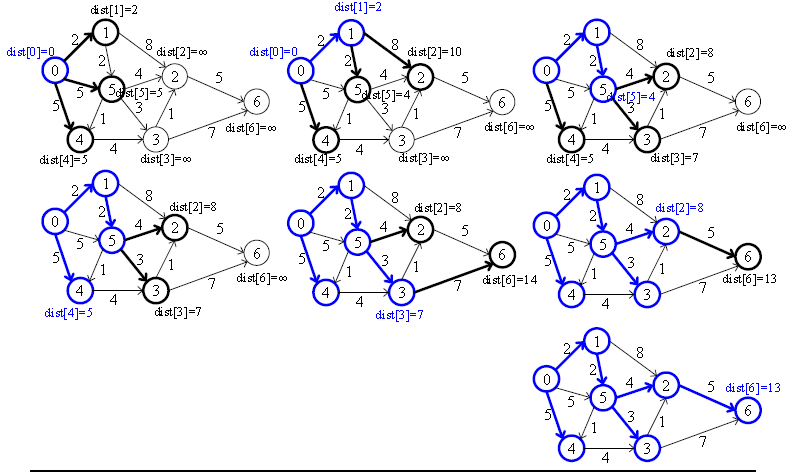
다익스트라 알고리즘은 큐 대신에 우선 순위 큐를 사용함으로써 이 문제를 해결한다.
너비 우선 탐색에서는 큐에 정점의 번호를 넣었지만
다익스트라 알고리즘에서는 우선순위 큐에 정점의 번호와 함께 지금까지 찾아낸 해당 정점까지의 최단 거리를 쌍으로 넣는다.
우선순위 큐는 정점까지의 최단 거리를 기준으로 정점을 배열함으로써,
아직 방문하지 않은 정점 중 시작점으로부터의 거리가 가장 가까운 점을 찾는 과정을 간단하게 해준다
우선 순위 큐를 사용한다는 점을 제외하면 다익스트라 알고리즘의 구조는 너비 우선 탐색과 비슷하다
각 정점까지의 최단 거리를 저장하는 배열 dist[]를 유지하며, 정점을 방문할 때마다 인접한 정점을 모두 검사한다.
간선 (u, v)를 검사했는데 v가 만약 아직 방문하지 않은 정점이라 해보자.
그러면 u까지의 최단 거리에 (u, v)의 가중치를 더해 v까지의 경로의 길이를 찾는다.
이것이 지금까지 우리가 찾은게 최단 거리라면 dist[v]를 갱신하고
(dist[v], v)를 큐에 넣는것이다.
여기서 dist[v]는 차후에 갱신될 수 있고 갱신되면 다시 이 경로에 의해 최소 경로길이가 생기는지 조사하기 위해
우선순위 큐에 집어넣는다 (갱신은 처음에만 일어난다. 그리디이기 때문).
- 이 코드는 방문한 정점과 방문하지 않은 정점을 구분하지 않기 때문에, q와 u사이에 음수 간선이 있다면, u를 다시 큐에 넣게된다.
이 경우 시간 복잡도가 정점의 갯수에 대해 지수적으로 증가할 수 있기 때문에 실제 음수 간선이 있는 그래프는 다익스트라를 안쓴다.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
|
const int MAX_V = 10;
int v;
vector<pair<int, int> > adj[MAX_V];
vector<int> dijkstra(int src)
{
vector<int> dist(v, INFINITY);
dist[src] = 0;
priority_queue<pair<int, int> > pq;
pq.push(make_pair(0, src));
while(!pq.empty())
{
int cost = -pq.top().first;
int here = pq.top().second;
pq.pop();
if(dist[here] < cost) continue;
for(int i = 0; i < adj[here].size(); i++)
{
int there = adj[here][i].first;
int nextDist = cost + adj[here][i].second;
if(dist[there] > nextDist)
{
dist[there] = nextDist;
pq.push(make_pair(-nextDist, there));
}
}
}
return dist;
}
|
cs |
위 그림의 그래프를 보면 bfs스패닝 트리처럼 트리형태가 생긴다.
6. 정당성의 증명
다익스트라 알고리즘은 bfs의 연장선상에서 고안되었기 때문에 최단 거리를 잘 계산할거라 예측할 수 있다.
다음은 귀류법을 통한 증명이다.
다익스트라 알고리즘이 최단 거리를 제대로 계산하지 못한 정점 u가 있다고 하자.
이런 정점이 두 개 이상인 경우, 그 중 첫 번째로 방문하는 정점을 선택한다.
시작점에서 시작점은 항상 최단 거리이기 때문에 u는 시작점이 아니다.
그러면 다익스트라 알고리즘이 u를 방문하는 순간,
u이전에 방문한 정점들과 아직 방문하지 않은 정점들로 그래프를 나눌 수 있다.
이때 u에 대해 최단 거리를 잘못 계산했다는 말은 다익스트라 알고리즘이 만든 스패닝 트리에서의 경로보다
더 짧은 경로가 존재한다는 의미이다.
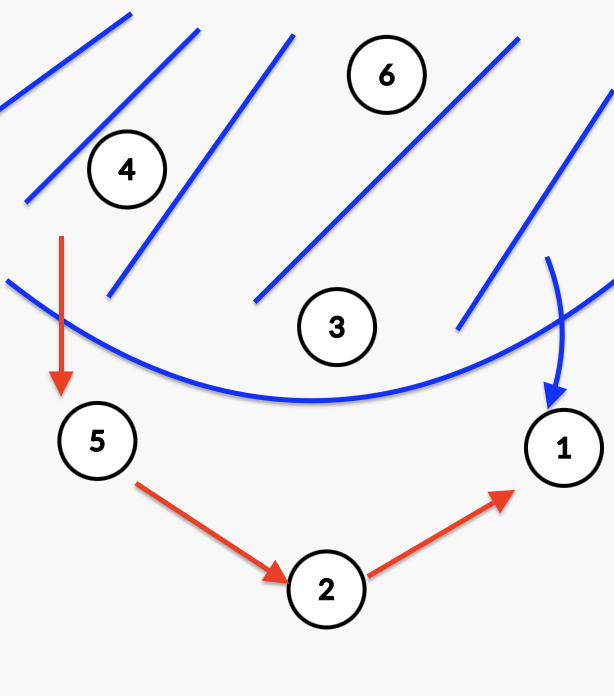
위 그림과 같이
만약 1 을 다음번에 조사한다고 하자, 하지만 이것은 최단 경로가 아니다라고 가정하자
그러면 방문된 부분에서 이어지는 아직 방문하지 않은 정점을 이어서 1까지 만드는 최단 경로가 있다는 뜻이다
그 최단 경로가 4->5 로 이어진다고 하자 그러면 distance[5] = distance[4] + w(4, 5) 이고 이는 우선순위 큐 안에 집어 넣어진다.
1을 우선 순위 큐에서 꺼내었다는 것은 distance[1] < distance[5] 라는 의미이다.
따라서 5에서 1로 이어지는 어떠한 경로들도 최소가 될 수 없다.
7. 시간 복잡도
위의 코드는 크게 두 부분으로 나누어 볼 수 있다.
1. 각 정점마다 인접한 간선들을 모두 검사하는 작업이고
2. 우선순위 큐에 원소를 넣고 삭제하는 작업이다.
각 정점은 정확히 한 번씩 방문되고, 따라서 모든 간선은 한 번씩 검사된다
그러므로 1번 부분은 O(|E|)의 시간이 걸린다
2번을 계산하기 위해서는 우선순위 큐의 최대 크기가 얼마가 되는지를 알아야한다.
bfs에서는 모든 정점이 큐에 한 번씩만 들어가기 때문에 큐의 최대 크기는 O(|V|)이다.
그러나 위 코드는 갱신할 때마다 원소를 우선 순위 큐에 넣기 때문에
그 보다 많은 원소들이 들어간다
우선순위 큐에 추가되는 원소의 수는 최대 O(|E|)가 된다.
여기서 원소의 삭제와 추가는 O(lg|E|)가 되고 이를 E만큼 하므로
O(|E|lg|E|)가 됨을 알 수 있다.
따라서 두 작업은 O(ElgE)가 되고 간선의 개수 |E|는 |V|^2 보다 작기 때문에 O(lg|E|) = O(lg|V|)라고 볼 수 있다.
따라서 위 코드의 시간 복잡도는 O(ElgV) 이다.
8. 실제 경로 찾기
너비 우선 탐색에서처럼 스패닝 트리를 만들어 거슬러 올라가면 경로를 찾을 수 있다.
9. O(|V|lg|V|)에 다익스트라 구현하기
중복 원소를 우선순위 큐에 넣지 않도록 수정하면 O(|V|lg|V|)시간에 동작한다
하지만 이는 피보나치 힙이나 이진 검색 트리를 이용해 우선순위 큐를 작성해야하므로
구현이 더 복잡해저 실제 수행에 더 느릴 수 있다.
피보나치 힙은 큐의 원소들의 크기를 조절할 수 있는 힙이다 - 구현에 드는 상수시간이 커서 실제 느리다
이진 검색 트리는 각 정점에 대해 찾고 삭제하고 다시 트리에 넣는 구조이다. 따라서 조금 비효율적임.
10. 우선순위 큐를 사용하지 않는 다익스트라 구현
정점의 수가 적거나 간선의 수가 매우 많은 경우에는
아예 우선순위 큐를 사용하지 않고 구현하는 방식이 더욱 빠른 경우가 있다
매번 반복문을 이용해 방문하지 않은 정점 중 거리가 가장 작은 걸 찾는다.
(이어지지 않은 것들은 무한대의 값을 가지므로 무시하면 결국 연결된것중에서만 찾는다.)
방문 여부를 배열로 기록해야한다.
이는 O(|V|^2 + |E|) 의 시간 복잡도를 가진다.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
|
const int MAX_V = 10;
int V;
vector<pair<int, int> > adj[MAX_V];
vector<int> dijkstra2(int src)
{
vector<bool> visited(V, false); vector<int> dist(V, INF);
dist[src] = 0; visited[src] = false;
while(true)
{
int closest = INF, here;
for(int i = 0; i < V; i++)
if(dist[i] < closest && !visited[i])
{
here = i; closest = dist[i];
}
if(closest == INF) break;
visited[here] = true;
for(int i = 0; i < adj[here].size(); i++)
{
int there = adj[here][i].first;
if(visited[there]) continue;
int nextDist = dist[here] + adj[here][i].second;
dist[there] = min(dist[there], nextDist);
}
}
return dist;
}
|
cs |
- 알고리즘 문제해결전략 930p
'알고리즘 > 알고리즘 정리' 카테고리의 다른 글
| [그래프] Graph 9: Floyd 플로이드의 모든 쌍 최단 거리 알고리즘 (0) | 2021.02.20 |
|---|---|
| [그래프] Graph 8: 벨만-포드 최단 경로 알고리즘 (0) | 2021.02.19 |
| [그래프] Graph6: BFS 양방향 탐색, IDS : 15-퍼즐 (0) | 2021.02.17 |
| [그래프] Graph 5: Breadth First Search 그래프의 너비 우선 탐색 (0) | 2021.02.16 |
| [그래프] Graph 4: DFS의 응용: 간선 분류-dfs 스패닝 트리, 절단점, 강결합 컴포넌트 분리 (2) | 2021.02.14 |