2021. 1. 6. 10:42ㆍ알고리즘/알고리즘 정리
동적 계획법이라는 말은 최적화 문제를 연구하는 수학 이론에서 왔다.
중복되는 부분 문제 없애 최적화하여 속도향상을 꾀하는 알고리즘 설계 기법이 바로 동적 계획법이다.
동적계획법은 분할 정복과 접근방식이 같다.
주어진문제 -> 더 작은문제들 -> 조각 계산 -> 조각의 답들로부터 원래 문제 답 계산
어떤 부분 문제는 두 개 이상의 문제를 푸는데 사용될 수 있기 때문에
여러번 계산하는 대신 한번만 계산하고 계산 결과를 재활용함으로써 속도 향상을 꾀함
각 문제의 답을 메모리에 저장해 둘 필요가 있음
이미 계산한 값을 저장해 두는 메모리의 장소를 캐시라고 부름
두번 이상 계산되는 부분문제를 부분 문제(overlapping subproblems)라고 부름
계산의 중복 횟수는 분할의 깊이가 깊어질 수록 지수적으로 증가하게 됨
따라서 두 번 이상 반복 계산되는 부분 문제들의 답을 미리 저장함
참조적 투명성(referential transparency):
함수의 반환 값이 그 입력 값만으로 결정되는지의 여부
참조적 투명 함수(referential transparent function):
입력이 고정되어 있을 때 그 결과가 항상 같은 함수
메모이제이션은 참조적 투명 함수의 경우에만 적용가능함
메모이제이션 구현패턴
- 항상 기저 사례를 제일 먼저 처리.
(입력이 범위를 벗어난 경우 등)
- 함수의 반환 값에 따라 cache[]를 초기화
(항상 0이상을 리턴하면 모두 -1로 초기화)
- cache[]가 다차원이상일때 참조형 변수를 따로 생성 -> 간결한 코드
- memset을 이용한 cache[]초기화
(정수 배열을 0 또는 -1로만 채울 수 있음)
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
|
int cache[2500][2500];
int someObscureFunction(int a, int b)
{
if(...) return ...;
int& ret = cache[a][b];
if(ret != -1) return ret;
return ret;
}
int main()
{
memset(cache, -1, sizeof cache);
}
|
cs |
메모이제이션의 시간 복잡도 분석
(존재하는 부분 문제의 수) * (한 부분 문제를 풀 때 필요한 반복문의 수행 횟수)
동적 게획법 레시피
1. 주어진 문제를 완전 탐색을 이용해 해결함
2. 중복된 부분 문제를 한 번만 계산하도록 메모이제이션 적용
반복적 동적 계획법
재귀 호출을 이용하지 않고 동적 게획법을 구현하는것
최적 부분 구조(optimal substructure)
동적계획법을 구현할 때 어떤 정보가 문제를 해결하는 데 아무 상관이 없다는 사실을 파악하여
지금까지 어떤 경로로 부분 문제에 도달했건 남은 부분 문제는 항상 최적으로 푸는 것
최적 부분 구조는 어떤 문제와 분할 방식에 성립하는 조건이다.
각 부분 문제의 최적해만 있으면 전체 문제의 최적해를 쉽게 얻어낼 수 있을 경우 이 조건이 성립한다.
최적 부분 구조가 성립함 = 각 부분문제 최적으로 품 -> 전체 문제 최적해 구함
최적화 문제 동적 계획법 레시피
1. 모든 답을 만들어 보고 그중 최적해의 점수를 반환하는 완전 탐색 알고리즘을 설계함.
2. 전체 답의 점수를 반환하는 것이 아니라, 앞으로 남은 선택들에 해당하는 점수만을 반환하도록 부분 문제 정의를 바꿈
3. 재귀 호출의 입력에 이전의 선택에 관련된 정보가 있다면 꼭 필요한 것만 남기고 줄임.
문제에 최적 부분 구조가 성립할 경우 이전 선택에 관련된 정보를 완전히 없앨 수 있음.
가능한 한 중복되는 부분 문제를 많이 만듦.
입력의 종류가 줄어들면 줄어들 수록 더 많은 부분 문제가 중복되고, 따라서 메모이제이션을 최대 한도로 활용함.
4. 입력이 배열이거나 문자열인 경우 가능하다면 적절한 변환을 통해 메모이제이션할 수 있도록 함.
5. 메모이제이션을 적용
최적화 문제의 실제 답 계산하기
1. 재귀함수에 실제 답을 도달하는 원소들을 담는 배열을 반환하도록 만든다
2. 실제 답을 계산하는 과정을 별도로 구현
어떤 선택지로 채울지 하나 하나 시도하면서 어떤 선택지를 택했을 떄 최적해를 얻는지 기록
최적화 문제 답 계산하기 레시피
1. 재귀 호출의 각 단계에서 최적해를 만들었던 선택을 별도의 배열에 저장해둠.
2. 별도의 재귀 함수를 이용해 이 선택을 따라가며 각 선택지를 저장하거나 출력.
k번째 답 계산하기 레시피
1. 답들을 사전순서대로 만들며 경우의 수를 세는 완전 탐색 알고리즘을 설계하고, 메모이제이션을 적용해 경우의 수를 세는 동적 계획법 알고리즘으로 바꿈.
2. 모든 답들을 사전순으로 생성하며 skip개를 건너뛰고 첫 번째 답을 반환하는 재귀 호출 함수를 구현.
재귀 함수는 각 조각들에 들어갈 수 있는 값을 하나씩 고려하면서
이 값을 선택했을 때 만들어지는 답의 수 M과
건너 뛰어야 할 답의 수 skip을 비교.
a) M <= skip: M개의 답은 모두 우리가 원하는 답보다 앞에 있어으므로, 이들을 건너뜀
대신 skip을 M만큼 줄임.
b) M > skip: M개의 답 중에 우리가 원하는 답이 있으므로, 이값을 선택.
M개의 답 중에 skip개를 건너뛴것이 답. 이 값을 답에 추가, 나머지 부분을 생성
정수 이외의 입력에 대한 메모이제이션
1. STL의 map과 같은 연관 배열을 사용해 캐시를 구현
ex) 입력이 정수 배열 -> map<vector<int>, int> cache;
컨테이너들을 사용하게 되면 시간이 오래걸리기 때문에
계산량이 아주 작은 문제에만 사용가능
2. 일대일 대응 함수 작성하기
입력을 정수로 변환해주는 함수
int cache[N_FACTORIAL];
int mapFoo(const vector<int>& key);
cache[mapFoo(key)]
일대일 대응 함수를 만들어야 하는 이유
- 만약 두 개의 다른 입력 a, b에 대해 반환 값이 같다면 잘못된 답을 반환할 수 있다.
- 어떤 배열 위치에 대응되는 입력이 없다면, 해당 위치는 버려지게 되어
프로그램이 필요한 것 보다 많은 메모리를 사용하게 됨
3. 입력값이 불린 값의 배열인 경우
배열의 입력의 수는 2^n가지가 된다.
길이 n인 배열을 길이가 n인 2진수로 본다.
index = 0 => 맨 아래 자리
index = n-1 => 가장 윗자리
n의 크기가 작을 때 사용
입력이 불린 값의 배열인 함수를 작성할 때 배열대신 정수를 전달하는 함수를 작성
-> 배열을 이진수로 바꿔주는 함수를 작성할 필요없음.
-> 배열의 값에 접근하려면 비트마스크를 이용해야해서 번거러움
-> 대신 입력 변환 부하가 줄어들어 전반적인 속도 유리
4. 입력이 순열인 경우
가능한 n!개의 입력들 중 X가 사전순으로 몇 번째 오는지를 계산하는 함수를 만들면
쉽게 메모이제이션할 수 있다.
//factorials[i] = i!
int factorials[12];
//X => [0..n-1] 의 순열 -> 사전순 번호 리턴 (0에서 시작)
int getIndex(const vector<int>& X)
{
int ret = 0;
for ( int i = 0 ; i < X.size() ; ++i )
{
int less = 0;
for ( int j = i + 1 ; j < X.size() ; ++j)
if( X[j] < X[i] )
++less;
ret += factorials[X.size() - i - 1] * less;
}
return ret;
}
5. 입력의 범위가 좁을 경우
길이 5 인 정수 배열이 각 값이 [ 0 , 9 ] 범위에 속한다고 하면
각 배열은 십진수 하나에 일대일로 대응 된다.
즉, 배열의 길이가 n이고 배열의 원소가 [0, k-1] 범위에 들어간다면,
이 입력을 n자리의 k진수로 볼 수 있다.
각 수가 나타내는 값을 배열의 인덱스로 쓰면 1:1대응이 성립한다.
조합 게임(combinatiorial game)
동적 계획법의 또 다른 사용처는 여러 조합 게임(체스. 바둑, 오목)을 해결하는 것이다.
'해결'한다는 말은 게임의 상태가 주어졌을 때 완벽한 한 수를 찾아내는 알고리즘을 만든다는 뜻이다.
조합 게임을 해결하는 알고리즘은 이와 같이 게임판이 주어질때 어느 쪽이 이길지를 미리 예측함.
이때 한쪽이 이긴다는 말은, 상대방이 어떻게 두더라도
자신이 실수만 하지 않는다면 반드시 이길 수 있다는 의미이다.
1. 게임 트리
모든 상태를 트리의 형태로 그린것
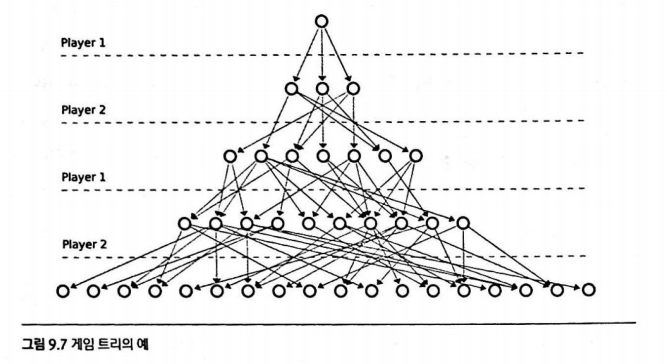
참가자가 둘 수 있는 수들: 정점에서 나가는 간선
결과적으로 얻을 수 있는 게임의 상태: 간선 끝 각 정점
완전한 게임 트리가 주어지면 우리는 어떤 게임도 완벽하게 풀 수 있다.
맨 아래 쪽, 최종 상태에서부터 거슬러 올라가면 된다.
2. 위에서 내려가기
게임 트리 전체를 그린 후 밑에서부터 승패를 판단하면서 올라가는 bottom up 알고리즘은
직관적이지만 구현하기 까다롭다.
맨 아래 줄에서 게임이 종료하는 것이 아니라 그 전에 승부가 나거나 트리가 구분이 잘 안될 수 도있다.
top down 재귀 호출 알고리즘은 다음과 같은 함수 정의를 이용한다.
winner (state, player) = 게임의 현재 상태가 state, player가 수를 둘 차례일 때 어느 쪽이 최종적으로 이기는지
유의할 점은 어느 쪽이 수를 둘 차례인지를 player 인자를 통해 따로 전달한다는 점이다.
= 게임의 상태만 가지고는 누가 둘 차례인지 알 수 없는 게임들인 경우
= impartial game 대칭 게임 정도: 각 참가자가 둘 수 있는 수가 완전 똑같다. ex) NIM
하지만 다음과 같이 정의를 바꿀 수 있다.
canWin(state) = 게임의 현재 상태가 state일 때, 이번에 수를 둘 차례인 참가자가 이기는지
이런 정의를 이용하면 구현이 더 직관적이 된다.
canwin은 둘 수 있는 수를 순회하며, 해당 수를 둔 후의 상태 state에 대해 canWin을 호출한다.
canWin(state) = true => 다음 차례가되는 상대방이 이김
canWin(state) = false => 내가 이김
따라서 false 를 반환 하는 수가 하나라도 있으면 이 상태에서 자신이 이길 수 있음을 나타냄.
3. 메모이제이션
위 그림에서 볼 수 있는 점은 한 정점에 도달할 수 있는 경로가 여러가지라는 것이다.
한 상태를 여러가지 방법으로 표현할 수 있어서 메모이제이션이 용이하다.
4. 게임 트리가 넓고 깊을 경우
바둑이랑 체스는 트리가 넓고 깊어서 컴퓨터로 계산하기 힘들다.
이와 같은 한계 때문에 실제 바둑이나 체스를 두는 인공지능 알고리즘들은
전체 게임 트리의 일부만 탬색한다.
이런 알고리즘은 대개 현 상태에서 둘 수 있는 모든 수를 시뮬레이션하는 것이 아니라
가장 그럴듯한 몇 개만을 시뮬레이션하고, 시간제한 내에 탐색할 수 있는 깊이에 도달하면
현재 상태가 나에게 얼마나 유리하고 불리한지 계산하는 함수를 이용하여 어느쪽을 선택하는지
판단한다.
이와 같은 방법들은 대개 경험적 알고리즘과 미니맥스 알고리즘등을 이용해 구현된다.
5. 처음으로 돌아올 수 있는 게임들
이 문제들은 게임 트리에 사이클이 생길 수 있기 때문에 쉽게 문제를 해결할 수 없다
(체스인 경우 50수 규칙에 의해 게임트리를 그릴 수 있다.)
반복적 동적 계획법 (iterative)
부분 문제 간의 의존성을 파악하기 쉬울 경우에는 재귀 함수가 아니라 반복문을 이용해서
동적 계획법을 구현할 수 있다.
슬라이딩 윈도를 이용한 공간 복잡도 줄이기 (sliding window)
반복적 동적 계획법의 유용한 사용처 중 하나는 경우에 따라 공간 복잡도를 줄이는데 쓸 수 있다는 것이다.
슬라이딩 윈도란 사용하는 데이터 전체를 메모리에 유지하는 것이 아니라 필요한 부분만을 저장하는 기법이다.
이 기법을 이용할때에는 만약의 경우에 대비해 실제 필요한 것보다 배열크기를 하나씩 더 잡는 습관을 들이면 좋다.
행렬 거듭제곱을 이용한 동적 계획법
굉장히 한정된 경우에만 쓸 수 있지만 반복적 동적 계획법을 이용한 매우 유용한 트릭.
선형변환(linear transform) 형태의 점화식을 행렬을 이용해 빠르게 푸는 기법.
ex) 피보나치 수열(fibonacci sequence)
피보나치 수열의 특정항을 구하는 문제:
피보나치 수열은 첫 두 숫자가 각각 0, 1 이고, 다음부터는 이전 두 수의 합으로 정의되는 두 수의 합으로
정의되는 무한 수열이다.
점화식은 다음과 같다.
fib(n) = fib(n-1) + fib(n-2)
이것을 단순하게 구현하자면 O(N)의 동적 계획법 알고리즘을 사용할 수 있다.
하지만 행렬 제곱 알고리즘을 사용하면 더욱 빨리 계산할 수 있다.

fib(i-1) 와 fib(i)를 포함하는 열벡터를 Ci라 하면
Ci+1 은 다음과 같다.
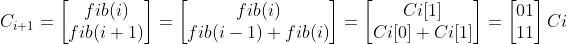
Ci+1을 Ci에 행렬의 곱으로 표현할 수 있다는 것이다.
즉
Cn = W^(n-1) * C1
이 식에서 W^n-1 을 행렬의 빠른 제곱을 써서 lgn 시간안에 구할 수 있고
C1에 바로 곱하면 답을 얻을 수 있다.
행렬 거듭 제곱 일반화
C(i , j)와 같이 두개의 인자를 받는 2차원 점화식으로 정의되는 동적 계획법 알고리즘이 있다고 하자
이때 [C(i , 0), C(i ,1), ... , C(i, m-1)] 의 열 벡터를 Ci라고 하자
문제에 따라 C(i, j)를 다음과 같이 Ci-1의 원소들의 가중치 합 , 곧 선형결합(벡터를 다 더한것)으로 쓸 수 있는 경우
에만 이 행렬 거듭 제곱을 써먹을 수 있다.
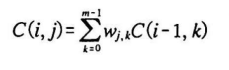
그러면 Ci를 다음과 같이 Ci-1에 행렬을 곱한 것으로 바꿔 슬 수 있다.
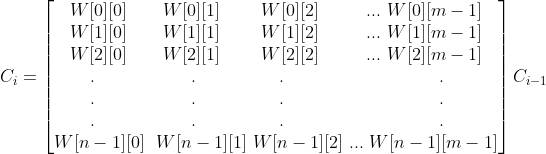
이제 이식은 다음과 같이 쓸 수 있다 : Cn-1 = W^n-1 C0
행렬의 빠른 제곱을 이용해 W^n-1을 O(m^3 lgn) 시간에 계산할 수 있게된다.
C(i, j)를 모두 반복적 동적 계획법으로 계산하려면 O(nm)개의 값을 각각 O(M) 시간이 걸려서 계산하니
O(nm^2)의 시긴이 걸린다.
그러므로 m 이 매우 작고 n이 엄청 클 때 이 방법은 효과적이다.
반복적 동적 계획법과 재귀적 동적 계획법의 비교
재귀적 동적 계획법의 장단점
1. 좀더 직관적
2. 부분 문제 간의 의존 관계나 계산 순서에 대해 고민할 필요가 없다
3. 전체 부분 문제 중 일부의 답만 필요할 경우 더 빠르게 동작
4. 슬라이딩 윈도 기법을 쓸 수 없다.
5. 스택오버플로를 조심해야한다.
반복적 동적 계획법의 장단점
1. 구현이 대개 더 짧다.
2. 재귀 호출에 필요한 부하가 없기 때문에 조금 더 빠르다
3. 슬라이딩 윈도 기법을 사용할 수 있다.
4. 구현이 좀더 비직관적이다.
5. 부분 문제간의 의존 관계를 고려해 계산되는 순서를 고민해야한다.
가능한 한 자신이 선택한 방향으로 일관되게 연습하자
- 알고리즘 문제해결전략 207p ~
--------------------------------------------------------------
최적 부분 구조..
잘 분리해야함
마지막 행동을 묶어내는 것이 중요
1. 문제정의.. 테이블 정의
dp[i][j] =
2. 의미 확인, DP를 끝냈을 때 나오는 값 (dp[N][K]))
3. 초깃값 설정
작은 -> 큰
(초기 -> )
4. 점화식
dp[i][j] = 1~i 번 물건을 고려해서 총 j만큼 무게 사용
- 첫번째 케이스 i번 안씀: dp[i-1][j] = 1~i-1 번을 고려해서 최대 가치
- 두번째 케이스 i번 씀: dp[i-1][j - w[i]] = 1~i-1 번 물건으로 무게 j-w[i] 만큼을 최대한 높이자
'알고리즘 > 알고리즘 정리' 카테고리의 다른 글
| [완전 탐색] Combinatorial search 조합 탐색 (0) | 2021.01.19 |
|---|---|
| [탐욕법] Greedy method (0) | 2021.01.18 |
| [비트 마스크] bitmask (0) | 2021.01.15 |
| [분할 정복] Divide & Conquer (0) | 2021.01.02 |
| [Brute-force] 완전 탐색 레시피 (0) | 2020.12.29 |