2021. 9. 18. 14:45ㆍ알고리즘/백준
1. 문제
https://www.acmicpc.net/problem/1533
1533번: 길의 개수
첫째 줄에 교차점의 개수 N이 주어진다. N은 10보다 작거나 같고, 시작점의 위치 S와 끝점의 위치 E, 그리고 정문이가 늦는 시간 T도 주어진다. S와 E는 N보다 작거나 같은 자연수이다. T는 1,000,000,000
www.acmicpc.net
2. 풀이
늦는 시간 T 동안 주어진 그래프에서 이동할 수 있는 길의 경우의 수 구하는 문제.
가중치가 1인 인접 행렬 그래프를 n번 제곱하면
(가중치가 없는)
mat[i][j]의 값은 i 에서 j 로가는 경로중 n개의 간선이 있는 경로의 경우의 수 와같다.
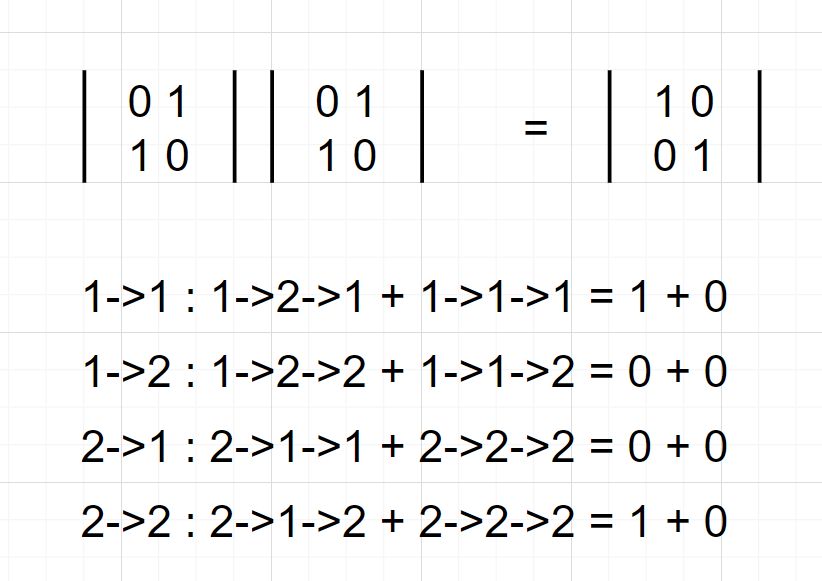
따라서 주어진 그래프를 가중치가 1 인 인접행렬 그래프로 변환하고
T 제곱 하면 간선의 개수가 T인 경로의 개수를 구할 수 있다.
여기서 간선의 의미는 간선을 지나갈때마다 1분이 소모된다는것을 의미하며,
늦는 시간 T에 딱맞추는 문제이므로 이러한 풀이 방법은 타당하다.
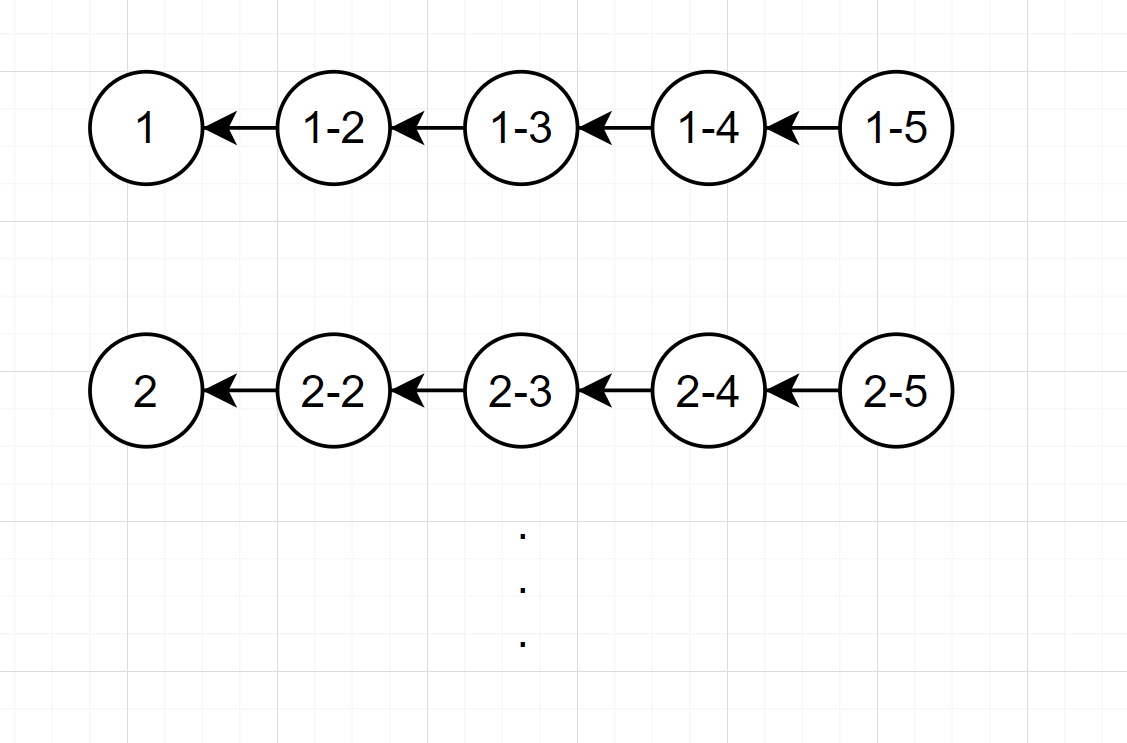
3. 그래프 변환
문제는 그래프를 변환하는것이다.
문제에서 주어진 가중치는 5 이하이다.
그러므로 가중치마다 정점을 생성하고 각 해당하는 가중치에 연결하면
적절한 크기의 가중치 없는 그래프를 만들 수 있다.
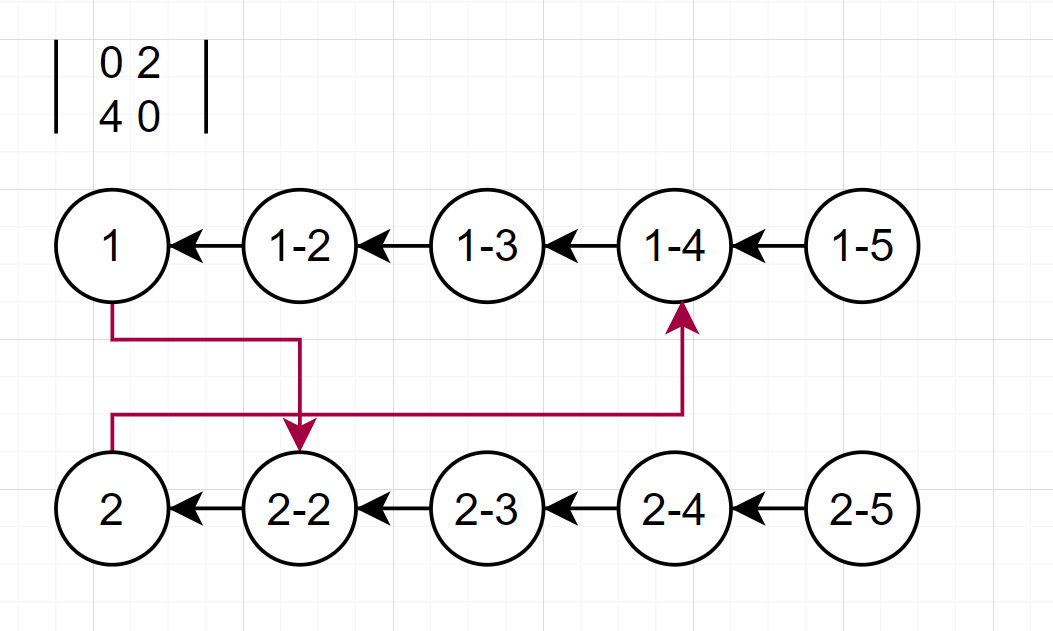
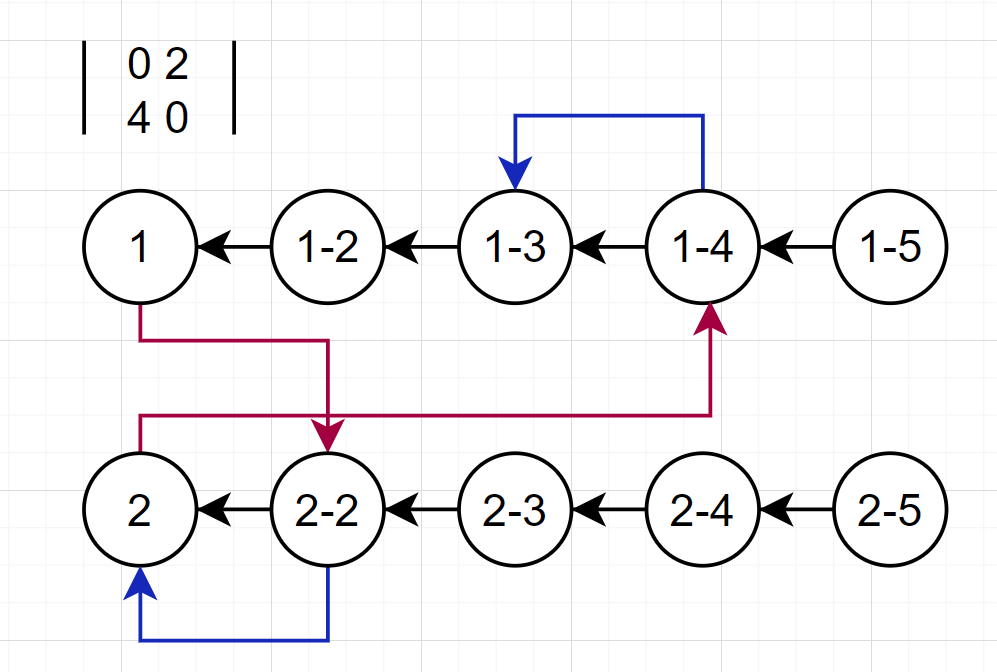
여기서 중요한 점은 각각의 가중치가 이전의 가중치를 가리켜야한다는것이다.
이와 같은 간선을 가지게 되면 제곱마다 다음 가중치로 가는 경우의 수에 반영되어
자연스럽게 답을 구할 수 있게 된다.
4. 분할정복을 이용한 행렬 제곱
행렬의 제곱은 분할정복을 사용하여 더 빠르게 할 수 있다.
A 라는 행렬이 있으면 A^4 는 다음과 같이 풀어 쓸 수 있다.
AxAxAxA
이제 이 식을 결합법칙에 의해 다음과 같이 다시 묶을 수 있다.
A^2 x A^2
또한 A^5 와 같이 홀수 제곱인 경우에도 마찬가지로 다음과 같이 묶을 수 있다.
A^4 x A
이런 패턴을 이용하여 절반씩 나누어 홀수인 경우에만 예외를 두면
더 빠르게 곱셈을 할 수 있다.
5. 코드
#include <iostream>
#include <algorithm>
#include <vector>
#include <map>
#include <cstring>
using namespace std;
using ull = unsigned long long;
int N{0};
int S{0};
int E{0};
int T{0};
const ull MOD = 1000003U;
ull base[50][50] = {0};
ull answ[50][50] = {0};
// 11 - 12 - 13 - 14 - 15
// 21 - 22 - 23 - 24 - 25
// 31 - 32 - 33 - 34 - 35
// ..
// s , e
void mulmat(ull lhs[50][50], const ull rhs[50][50])
{
ull ret[50][50] = {0};
int size = N * 5;
for (int i = 0; i < size; i++)
{
for (int j = 0; j < size; j++)
{
for (int v = 0; v < size; v++)
{
ret[i][j] += lhs[i][v] * rhs[v][j];
ret[i][j] = ret[i][j] % MOD;
}
}
}
memcpy(lhs, ret, 50 * 50 * sizeof ret[0][0]);
}
void pow(ull mat[50][50], int t)
{
if (t == 1)
{
memcpy(mat, base, 50 * 50 * sizeof mat[0][0]);
}
else if (t % 2 == 1)
{
pow(mat, t - 1);
mulmat(mat, base);
}
else
{
pow(mat, t / 2);
mulmat(mat, mat);
}
}
int solve()
{
pow(answ, T);
return answ[5 * S][5 * E];
}
/*
3 1 3 5
012
201
120
*/
int main()
{
ios_base::sync_with_stdio(0);
cin.tie(0);
cin >> N >> S >> E >> T;
S--, E--;
for (int i = 0; i < N; i++)
{
for (int j = 1; j < 5; j++)
{
base[i * 5 + j][i * 5 + j - 1] = 1;
}
}
for (int i = 0; i < N; i++)
{
for (int j = 0; j < N; j++)
{
char w;
cin >> w;
w -= '0';
if (w != 0)
{
base[i * 5][j * 5 + w - 1] = 1;
}
}
}
cout << solve();
}
'알고리즘 > 백준' 카테고리의 다른 글
| [백준] [C++] 5419번 북서풍 (seg tree, sweeping) (0) | 2021.10.16 |
|---|---|
| [백준][C++] 20036번 Ball Alignment (dp) (0) | 2021.10.07 |
| [백준][C++] 4206번 피보나치 단어 (dp, kmp) (0) | 2021.08.30 |
| [백준] [C++] 11400번 단절선 (dfs) (0) | 2021.07.22 |
| [백준] [C++] 11266번 단절점 (dfs) (0) | 2021.07.21 |