2021. 1. 23. 18:07ㆍ알고리즘/알고리즘 문제 [hard]
1. 기하
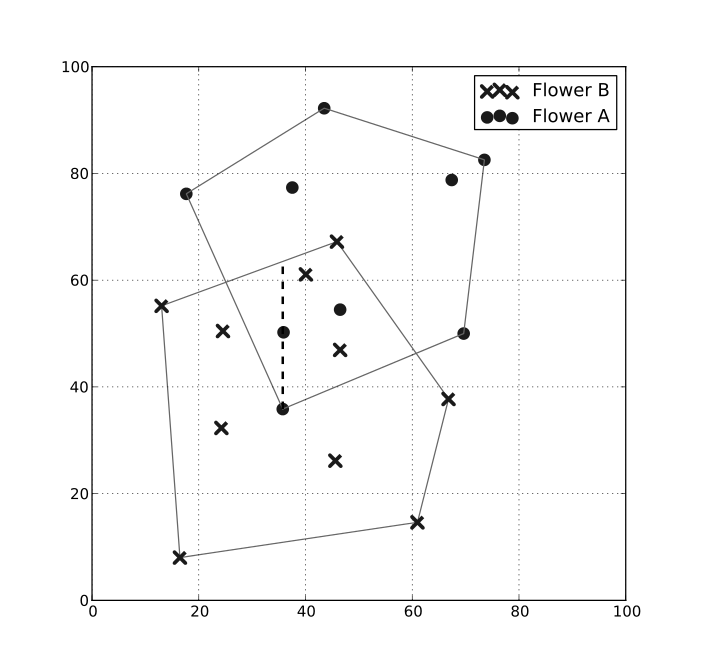
이 문제는 위와 같이 블록 껍질이 주어졌을 때
겹치는 다각형의 최대 수직 거리를 구하는 문제이다.
기하적으로 푸는 법은 다음과 같다.
- 교차되는 직선들의 교차점을 포함하고 두 블록 껍질의 교집합인 점들을 포함하는 블록껍질을 구한다.
- 구한 교집합 블록껍질의 꼭지점들을 X좌표에서 수직을 그어 최대인 수직 거리를 구한다.
(블록 껍질에서의 최대 수직 거리는 항상 꼭지점에서 그은 수직선이다. 기울기가 꼭짓점에서 바뀌기 때문이다.)
먼저 블록껍질의 점 하나를 다른 블록껍질의 선분들에 대응하면서 포함되는지 확인 해야 한다.
교집합이 될 수 있는 점의 범위를 최소화 하여 포함되는지 확인하자.
A와 B의 X값의 최대 최소를 비교하여 X값의 범위를
A와 B의 Y값의 최대 최소를 비교하여 Y값의 범위를
줄여서 비교해야할 점을 최소화할 수 있다.
두 A B껍질이 나란히 있을 경우
X값의 최대 최소점에서 시계나 반시계 방향으로 돌려서 교집합에 해당하는 점과 선분을 얻어낼 수 있을것이다.
두 A B껍질이 위 아래로 있을 경우
Y값의 최대 최소점에서 시계나 반시계 방향으로 돌려서 교집합에 해당하는점과 선분을 얻어 낼 수 있을 것이다.
하지만 주어진 데이터를 가지고 어느 형태로 겹치는지 바로 알 수 없다.
그러므로 줄어든 범위의 점을 하나 하나 조사 하는게 더 효율적일 것이다.
이는 최대 A*B의 시간이 걸린다.
만들어진 교집합은 아마 입력으로 주어진 것 처럼 친절하게 시계반대방향으로 나타나진 않을 것이다.
그러므로 이것을 시계반대방향으로 정렬을 해야한다.
이것은 컨벡스 헐 알고리즘으로 nlgn의 시간이 걸릴 것이다.
(선분을 구하기 위해 필요하다, 어느 형태로 겹치는지 알 수 있으면 반시계방향으로 교집합을 구할 수 있으므로 정렬은 필요없다.)
정렬을 한 뒤 꼭지점들에서 수직을 그어 만나는 선분과의 길이를 모두 구하고 최대값을 구하면
답을 얻어 낼 수 있다.
2. 블록 껍질 수직 거리 함수
삼분법으로 답을 구하기 위해서는 일단
교집합의 다각형에서 수직선분의 길이가 유니모달 함수를 이루는지 확인해야한다.
블록 껍질의 교집합은 블록 껍질이라는 것을 직관적으로 알 수 있다.
블록껍질은 수직 거리는 x의 맨 왼쪽에서 0이 되고
중심으로 갈수록 점점 길어진다.
이후 어느 한 꼭지점에서 최대가 된후
이는 점점 줄어들들다 맨 오른쪽에서 0이된다.
어느 한 꼭지점에서 최대가 되는 이유는 기울기가 변환되는 지점이기 때문이다.
기울기가 수직거리를 더 길게 만드는 쪽이라면 최대값은 이후 꼭지점에서 생길 가능성이 생기는 것이고
수직거리를 더 짧게 만드는 쪽이라면 이곳이 최대라는 것이다
또한 만약 수직거리를 더 짧게 만드는 기울기 다음 꼭짓점에서 다음 꼭짓점이 최대가 되는 경우라면
이 다각형은 블록 껍질이라 부를 수 없다. 이전 꼭지점과 다음꼭짓점을 연결하여 더 짧게 만드는 꼭짓점을 없앨 수 있기 때문이다.
따라서 블록껍질의 수직거리 함수는 유니모달함수이며
이는 삼분법을 이용하여 최대 수직거리를 구할 수 있음을 의미한다.
3. 삼분법
두 볼록껍질을 A와 B라하자
삼분법을 이용하기 위해서
lo 와 hi의 범위를 일단 정해야한다.
이는 수직 거리를 구하는 문제이므로 범위는 x축 이어야한다.
또한 [lo, hi] 구간에서는 A,B가 동시에 존재햐야한다.
동시에 존재하는 구간은
lo = A의 최소 x와 B의 최소 x 중 최대인 x
hi = A의 최대 x와 B의 최대 x 중 최소인 x
만약 동시에 존재하지 않은 경우 lo > hi가 되어 교집합이 생성하지 않아
수직거리는 0이된다.
이제 동시에 존재하는 구간을 정했으므로
삼분법을 통해 x 값들을 대입하여 최대가 될 수 없는 구간을 삭제해나가면 된다.
4. 수직거리
x값이 주어지면 수직거리를 구하는 함수를 만들어야한다.
한 블록 껍질에서 수직 거리는
x에서 윗껍질과 만나는 점의 y 좌표랑 아래 껍질에서 만나는 점의 y좌표를
뺀값과 똑같다.
이를 이용하여 두개의 블록 껍질을 하나의 윗껍질 벡터와 하나의 아래껍질 벡터로
분리하게 되면 계산하기가 더 수월해진다.
특정 x 좌표에는 두개의 윗껍질 선분 과 두개의 아래껍질 선분이 있다.
이는 A와 B 각각의 것이므로 분리하여 같이 저장해도 상관 없다.
이제 교집합의 수직거리를 구하기는 쉽다.
x가 주어졌을 때 두가지 상황이 있다.
x의 좌표에서 교집합이 생길 때:
두 윗 블록 껍질중 작은값 과 두 아래 블록 껍질 중 큰 값을 빼면 수직 거리가 나온다.
x의 좌표에서 교집합이 생기지 않을 때:
두 윗 블록 껍질중 작은값과 두 아래 블록 껍질 중 작은 값을 빼면 음수 값이 나온다.
식으로 표현해보자면
up(x) = 윗 껍질 중에서 x를 포함하는 윗껍질 벡터를 반환한다.
down(x) = 아래 껍질 중에서 x를 포함하는 아래 껍질 벡터를 반환한다.
vertical(x) = min(up(x)) - max(down(x))
이제 수직거리를 얻어낼 수 있으므로
삼분법을 통해 답을 얻어 낼 수 있다.
'알고리즘 > 알고리즘 문제 [hard]' 카테고리의 다른 글
| [트리] [x]INSERTION 삽입 정렬 뒤집기 (0) | 2021.02.06 |
|---|---|
| [트리] [시도 x]FORTRESS 요새 (0) | 2021.02.04 |
| [결정 문제] [시간 초과] WITHDRAWAL 수강 철회 (0) | 2021.01.22 |
| [조합 탐색][시도x]BOARDCOVER2 게임판 덮기2 (0) | 2021.01.20 |
| [탐욕법] [시도x] MINASTIRITH 미나스 아노르 (0) | 2021.01.19 |