2021. 1. 26. 20:58ㆍ알고리즘/알고리즘 정리
계산 기하
점, 선, 다각형, 원 등 각종 기하학적 도형을 다루는 알고리즘을
계산 기하 알고리즘이라고 한다.
알고리즘 문제들에서는 대부분 기초적인 수학 이론을 구현할 수 있는 능력을 평가한다.
2차원 기하학
벡터의 구현(vector)
방향과 거리를 모두 알고 있으면 두 점 사아의 상대적인 위치를 정확히 표시할 수 있다.
이런 방향과 거리의 쌍을 벡터라고 한다.
벡터는 수학, 물리학, 공학 전반에 걸쳐 널리 쓰이는 개념으로 가장 기초적인 도구이다.
벡터의 시작점을 바꿔도 벡터는 변하지 않기 때문에
항상 원점으로 정해두면 벡터를 끝점의 위치(x, y)로만 표현할 수 있다.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
|
#pragma once
#include <algorithm>
#include <cmath>
#include <limits>
#include <cfloat>
namespace VECTOR2
{
const double PI = 2.0* acos(0.0);
struct vector2
{
double x, y;
explicit vector2(double x_ = 0. ,double y_ = 0) : x(x_), y(y_)
{}
bool operator == (const vector2& rhs) const {
return x == rhs.x && y == rhs.y;
}
bool operator < (const vector2& rhs) const {
return x != rhs.x ? x < rhs.x: y < rhs.y;
}
vector2 operator + (const vector2& rhs) const {
return vector2(x + rhs.x, y + rhs.y);
}
vector2 operator - (const vector2& rhs) const {
return vector2(x-rhs.x, y-rhs.y);
}
vector2 operator * (double rhs) const {
return vector2(x*rhs, y*rhs);
}
double norm() const {return hypot(x, y);} //벡터의 길이
vector2 normalize() const {
return vector2(x/norm(), y/norm());
}
double polar() const { return fmod(atan2(y,x)+2*PI, 2*PI);}
double dot(const vector2& rhs) const {
return x*rhs.x + y*rhs.y;
}
double cross(const vector2& rhs) const {
return x*rhs.y - rhs.x*y;
}
vector2 project(const vector2& rhs) const {
vector2 r = rhs.normalize();
return r * r.dot(*this);
}
//반시계-> 양수
double ccw(vector2 a, vector2 b) {
return a.cross(b);
}
double ccw(vector2 p, vector2 a, vector2 b) {
return ccw(a - p, b - p);
}
//두직선의교차점
// p = (c-a) x dir2 / dir1 x dir2
bool lineIntersection(vector2 a, vector2 b, vector2 c, vector2 d, vector2& p) {
vector2 dir1 = b-a;
vector2 dir2 = d-c;
double det = dir1.cross(dir2);
if(fabs(det) < DBL_EPSILON) return false;
p = a + dir1*((c-a).cross(dir2)/det);
return true;
}
//평행한 두 선분일때 한점에서겹치는지확인
bool parallelSegments(vector2 a, vector2 b, vector2 c, vector2 d, vector2& p) {
if(b < a) std::swap(a, b);
if(d < c) std::swap(c, d);
if(ccw(a, b, c) != 0 || b < c || d < a) return false;
if(a<c) p = c; else p = a;
return true;
}
bool inBoundingRectangle(vector2 p, vector2 a, vector2 b) {
if (b < a) std::swap(a, b);
return p==a || p==b || (a < p && p < b);
}
bool segmentIntersection(vector2 a, vector2 b, vector2 c, vector2 d, vector2& p) {
if(!lineIntersection(a, b, c, d, p))
return parallelSegments(a, b, c, d, p);
return inBoundingRectangle(p, a, b) &&
inBoundingRectangle(p, c, d);
}
bool segmentIntersects (vector2 a, vector2 b, vector2 c, vector2 d) {
double ab = ccw(a, b, c) * ccw(a, b, d);
double cd = ccw(c, d, a) * ccw(c, d, b);
if(ab == 0 && cd == 0) {
if(b < a) std::swap(a, b);
if(d < c) std::swap(c, d);
return !(b < c || d < a);
}
return ab <= 0 && cd <= 0;
}
vector2 nomalVector(){
return vector2(-y,x).normalize();
}
double howMuchCloser(vector2 p, vector2 a, vector2 b){
return (b-p).norm() - (a-p).norm();
}
vector2 perpendicularFoot(vector2 p, vector2 a, vector2 b) {
return a + (p-a).project(b-a);
}
double pointToLine(vector2 p, vector2 a, vector2 b) {
return (p - perpendicularFoot(p, a, b)).norm();
}
};
}
|
cs |
1. 벡터의 덧셈, 뺄셈, 곱셈
두 벡터 a, b가 있다하자
|
1
2
3
4
5
6
7
8
9
|
vector2 operator + (const vector2& rhs) const {
return vector2(x + rhs.x, y + rhs.y);
}
vector2 operator - (const vector2& rhs) const {
return vector2(x-rhs.x, y-rhs.y);
}
vector2 operator * (double rhs) const {
return vector2(x*rhs, y*rhs);
}
|
cs |
- a + b 는 b의 시작점을 a의 끝점으로 옮겼을 때 a의 시작점에서 b의 끝점으로 끝나는 벡터이다.

- a - b 는 b의 끝점에서 a의 끝점으로 가는 벡터이다.( a - b= a + (-b))
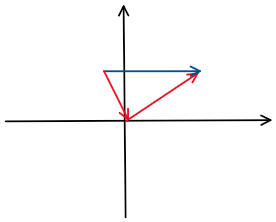
- a * r은 a의 길이를 r배로 늘린 벡터이다.
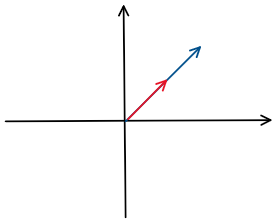
2. 벡터의 비교연산
|
1
2
3
4
5
6
|
bool operator == (const vector2& rhs) const {
return x == rhs.x && y == rhs.y;
}
bool operator < (const vector2& rhs) const {
return x != rhs.x ? x < rhs.x: y < rhs.y;
}
|
cs |
- 이와 같은 대소비교는 x의 좌표가 작은 벡터일 수록, 끝점의 x좌표가 같을경우 y좌표가 작을 수록
더 작은 벡터라고 계산한다.
이와 같은 구현은에는 수학적의미는 없지만 여러 알고리즘에서 유용하게 사용된다.
(두 선분의 교차 여부, 일직선상에서 점 비교)

3. 벡터의 극 각도 계산(polar angle)
|
1
|
double polar() const { return fmod(atan2(y,x)+2*PI, 2*PI);}
|
cs |
벡터의 극 각도란 해당 벡터의 방향이 x 축의 양의 방향으로부터 반 시계 방향으로 얼마나 차이나는지를
나타낸다.
atan2(y, x) : (y,x)좌표가 주어질 때 각 좌표의 부호를 이용해 각도를 계산 [-pi ,pi]
fmod(a,b): 실수 a를 b로 나눈 나머지. =>[0, 2pi) 로 구간값 변경
4. 벡터의 내적과 외적
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
|
double dot(const vector2& rhs) const {
return x*rhs.x + y*rhs.y;
}
double cross(const vector2& rhs) const {
return x*rhs.y - rhs.x*y;
}
vector2 project(const vector2& rhs) const {
vector2 r = rhs.normalize();
return r * r.dot(*this);
}
double ccw(vector2 a, vector2 b) {
return a.cross(b);
}
double ccw(vector2 p, vector2 a, vector2 b) {
return ccw(a - p, b - p);
}
vector2 perpendicularFoot(vector2 p, vector2 a, vector2 b) {
return a + (p-a).project(b-a);
}
double pointToLine(vector2 p, vector2 a, vector2 b) {
return (p - perpendicularFoot(p, a, b)).norm();
}
|
cs |

- 백터의 내적: 스칼라 리턴
a·b = ax * bx + ay * by = |a|*|b|*cosθ (코사인 법칙)
벡터의 사이각을 구할 때 사용: θ = acos(a·b /|a|*|b|)
벡터의 직각 여부 확인할 때: 내적이 0 이면 항상 직각이다.
벡터의 사영: 15.2 (a)처럼 내적에 |b|를 나눠주면 사영 값이나온다.
- 벡터의 외적: 벡터 리턴
a X b = ax * by - ay*bx = |a|*|b|sinθ (a,b의 평행사변형 넓이)
벡터의 외적은 3차원 벡터에 대해 정의되는 연산이다.
3차원 벡터 a, b가 주어졌을 때 이 두 벡터에 모두 수직인 다른 벡터를 반환한다.
2차원 벡터는 z값이 0인 3차원으로 생각할 수 있기 때문에, 외적을 사용할 수 있다.
면적계산:
외적의 크기는 평행사변형의 넓이이다, 이를 이용해 삼각형의 넓이를 쉽게 구할 수 있고,
응용하여 여러 다각형들의 넓이 또한 쉽게 구할 수 있다.
벡터의 길이와 방향:
aXb = -bXa
외적은 어느 방향으로 계산하느냐에 따라 그 부호가 달라진다.
sin-θ = -sinθ
θ가 a에서 b까지 반시계 방향으로 얼마나 회전하는가를 나타내기 때문이다.
따라서 외적이 음수인지 양수인지를 알면 각도가 양수인지 음수인지 알 수 있다.

aXb > 0 : b가 a로부터 반시계 방향으로 180도 이내
aXb < 0 : b가 a로부터 시계 방향으로 180도 이내
=> ccw(a, b)
점과 직선 사이의 거리
a, b점을 지나는 직선과 점 p의 거리를 구하는 방법은
p가 이 직선에 내리는 수선의 발을 계산한 뒤 그것과 p의 길이를 구하는 것이다.
내적을 사용하여 쉽게 구할 수 있다.
직선 선분 교차와 거리 면적
직선과 직선의 교차
직선을 한 점과 방향 벡터 즉, a + p * b (p는 실수) 형태로 표현하면 간단하게 구현할 수 있다.
a+p*b, c+q*d의 교점을 구하기 위해서는
a+p*b = c+q*d 방정식을 풀면된다.
1: ax + p*bx = cx + q*dx
2: ay + p*by = xy + q*dy
1식을 q에대해 정리하고 2식에 대입하면 p에대해 정리할 수 있다.
p = ((cx - ax)*dy - (cy - ay)*dx) / (bx*dy - by*dx)
p = (c-a)Xd / bXd
이를 a + pb에 대입해 원하는 점을 구할 수 있다.
bool lineIntersection(vector2 a, vector2 a1, vector2 c, vector2 c1, vector2& x) {
vector b = a1-a;
vector d = c1 -c;
double bXd = b.cross(d);
if(fabs(bXd) < EPSILON) return false;
double p = (c - a).cross(d)/bXd;
x = a + b * p;
return true;
}선분과 선분의 교차
1. 두 선분이 겹치지 않음.
2. 두 선분이 한 점에서 닿음.
3. 두 선분이 겹쳐짐.
4. 한 선분이 다른 선분 안에 포함됨.
위와 같은 유의점을 조심하여 두 직선의 교차점을 계산한 뒤 이 교차점이 선분위에 오는지 확인하면된다.
// 겹칠경우 교차점 하나를 찾는다.
bool parallelSegments(vector2 a, vector2 b, vector2 c, vector2 d, vector2& p) {
if (b < a) swap(a, b);
if (d < c) swap(c, d);
if(ccw(a, b, c) != 0 || b < c || d < a) return false;
if(a < c) p = c; else p = a;
return true;
}
//a b p 가 일직선상에 있을 때 p가 a-b 사이에 있는지
bool inBoundingRectangle(vector2 p, vector2 a, vector2 b) {
if(b < a) swap(a, b);
return p == a|| p == b || (a < p && p < b);
}
bool seqgmentIntersection(vector2 a, vector2 b, vector2 c, vector2 d, vector2& p) {
//직선 직선 평행하면.
if(!lineIntersection(a, b, c, d, p);
return parallelSegments(a, b, c, d, p);
return inBoundingRectangle(p, a, b) &&
inBoundingRectangle(p, c, d);
}선분 끼리의 교차점을 구하지 않고 여부만 확인
a-b, c-d 의 교차 여부를 확인하는 방법은 외적을 사용하는 것이다.
두 선분이 교차한다는 것은
a를 기준으로 c와 d 중 하나는 b의 시계방향, 하나는 b의 반시계방향에 있어야 함을 의미한다.
즉, ccw(a, b, c) * ccw(a, b, d) <= 0 , ccw(c, d, a) * ccw(c, d, b) <= 0 야 한다.
(평행할 때 교점이 생기는지 확인해야하고, 끝점에서 만나는 경우 또한 생각해야한다.)
bool segmentIntersects(vector2 a, vector2 b, vector2 c, vector2 d) {
double ab = ccw(a, b, c) * ccw(a, b, d);
double cd = ccw(c, d, a) * ccw(c, d, b);
if(ab == 0 && cd == 0) {
if(b<a) swap(a,b);
if(d<c) swap(c,d);
return !(b<c||d<a);
}
return ab <= 0 && cd <= 0;
}다각형(polygon)
다각형은 현실 세계를 계산 기하로 표현하는 데 필수적인 요소이다.
-블록 다각형 (convex polygon) 이란 모든 내각이 180도 미만인 다각형을 이야기한다.
두 블록 다각형의 교집합은 항상 볼록 다각형
블록 다각형 내부의 두 점을 연결하는 선분은 블록 다각형의 경계를 절대 교차하지 않는다.
-오목 다각형 (concave polygon) 이란 내각이 180도를 넘는 것을 가지는 다각형이다.
-단순 다각형 (simple polygon) 다각형의 경계가 스스로 교차하지 않는 다각형.
블록 다각형 면적 구하기
벡터의 외적을 이용하면 삼각형의 세 점이 주어딜 때 그 면적을 구할 수 있다.
이것을 응용하면 볼록 다각형의 면적을 쉽게 구할 수 있다.
내부의 한점을 잡고 반시계방향으로 연속된 두점으로 이루어진 선분을 가지는 삼각형을 구하면
결국 다각형의 면적을 구하게 된다.
오목 다각형 면적 구하기
벡터의 외적은 방향에 따라 부호가 바뀐다.
이는 오목 다각형의 면적을 구하는데에 중요한 역활을 한다.
오목 다각형의 점들이 반시계 순서대로 배열되어있다고 하면
바깥의 한 점 q를 잡고 인접한 두점 pi, p(i+1)%n 과 q 로 이루어진 삼각형의 넓이를
각각 외적으로 계산해 더한다.
이렇게 계산하게되면 음수 면적을 가진 삼각형이 생기게 되고 이것은
외부의 점을 잡아 생기는 오목 다각형 외부에 생긴 다각형과 상쇄되어
온전히 오목 다각형의 면적을 구하게 해준다.
double area(const vector<vector2>& p) {
double ret = 0;
for(int i = 0; i < p.size(); ++i) {
int j = (i+1)%p.size();
ret += p[i].x * p[j].y - p[j].x * p[i].y;
}
return fabs(ret) / 2.0;
}
내부/ 외부 판별
내부에 있는 점 q 에서 오른쪽으로 나아가는 반직선을 그으면
반직선은 홀수번 다각형의 변과 교차한다.
만약 변과 교차하지 않고
점에서 만나거나 변과 완전히 겹치는 경우가 있으면
엄청나게 작은 값만큼 반직선을 올려 판단하면된다.
(점에서 만난경우 만나는 변이 2개있다고 판단하여 잘못된 결과가 나올 수 있다.)
//q가 다각형의 경계위에 있는 경우는 정해지지 않음.
//반직선과 수평인 다각형의 변들은 무시된다.
bool isInside(vector2 q, const vector<vector2>& p) {
int crosses = 0;
for (int i = 0; i < p.size(); i++)
{
int j = (i+1) % p.size();
// q의 반직선이 선분 윗쪽 점과 겹칠경우 true 아래쪽점과 겹칠경우 false -> 한번만 셈
if((p[i].y > q.y) != (p[j].y > q.y))
{
double atx = (p[j].x - p[i].x) * (q.y - p[i].y) / (p[j].y - p[i].y) + p[i].x;
if(q.x < atX) crosses++;
}
}
return crosses % 2 > 0;
}
블록 껍질 모델링
1. 선물 포장 알고리즘 (gift wrapping algorithm)

선물 포장 알고리즘은 우선 항상 블록 껍질에 포함될 수 밖에 없는 점을 하나 찾아낸다.
그리고 그 점에 가상의 반직선을 붙인 뒤
이 반직선을 시계 반대 방향으로 돌리며
다른 점들을 감싸나간다.
1. 블록 껍질에 포함될 수 밖에 없는 점은 가장 왼쪽에 있는 점이다.
이는 vector2에 구현된 < 연산자를 이용하면 쉽게 정렬하여 찾을 수 있다.
2. 이후 모든 점에 대해서 조사를 한뒤 가장 왼쪽에 있는 것을 선택해나간다.
N개의 점이 있고 H개가 포함된다하면
이 알고리즘은 한번 호출될 때마다 N개를 조사하고 H번 호출되므로
O(NH)의 시간 복잡도를 가진다.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
|
typedef vector<vector2> polygon;
//points을 포함하는 최소 블록 다각형을 찾는다.
polygon gifWarp(const vector<vector2>& points) {
int n = points.size();
polygon hull;
vector2 pivot = *min_element(points.begin(), points.end());
hull.push_back(pivot);
while(true) {
vector2 ph = hull.back(), next = points[0];
for(int i = 1; i < n; ++i) {
// cross: 전에 선택한것을 기준으로 i번째 점이 후보에 반시계방향에 있을시 (왼쪽에 있을시) 업데이트.
double cross = ccw(ph, next, points[i]);
// dist: 평행할 때 지금보다 더 멀리 떨어저있는거라면 업데이트 시키라는 것.
double dist = (next - ph).norm() - (points[i] - ph).norm();
if(cross > 0 || (cross == 0 && dist < 0))
next = points[i];
}
if(next == pivot) break;
hull.push_back(next);
}
return hull;
}
|
cs |
2. 그라함 스캔(graham scan)
-모든 점을 탐색해 y축이 가장 낮은것 부터 시작한다.(p[0]으로 설정)
y축이 똑같을 시 x축이 작은것을 선택한다.
-나머지 n-1개의 점을
p[0] 기준으로 모든점과의 각도를 측정하고
시계반대 방향으로 정렬한다.
만일 각도가 같을 시 가까운거 먼저 넣는다.
-정렬후
같은 각도를 가지는 점들을 찾아
p[0]과 가장 먼점을 제외하고 나머지는 삭제한다.
삭제하고 난 나머지점들의 배열 크기들을 m이라 하자.
-m이 3보다 작을 시 블록껍질이 생성되지 않으므로 함수를 반환한다.
-stack S를 만들어 p[0] p[1] p[2]를 넣는다
-나머지 m-3개의 점들을 하나씩 다음과 같이 처리한다.
p[i]을 조사하여 p[i]과 스택들에 있는 원소들을 비교해본다.
ccw(S[top-1] , S[top], p[i]) => 반복문을 통해 시계반대 방향이 아니면 S.pop() 을 계속한다.
시계반대방향이면 반복문을 종료하고 S.push(p[i])
이 알고리즘은 정렬하는 시간에 지배되어 O(NlgN)이 된다.
따라서 선물포장 알고리즘 보다 더 많은 점들을 처리할 때 쓰인다.
선형 분리(linear separability)
2차원 공간 상에 주어진 두 종류의 점들을 구분하는 직선이 존재하는지 여부를 찾는 문제.
계산 기하 알고리즘 디자인 패턴
계산 기하 알고리즘 디자인 패턴
평면 스위핑(plane sweeping) or 라인 스위핑(line sweeping)
가장 유명한 계산 기하 알고리즘 디자인 패턴.
수평선 혹은 수직선으로 주어진 평면을
쓸고 지나가면서 문제를 해결한다.
(변화가 있는지점 = 이벤트)
(직사각형 합집합의 면적- 직사각형들의 좌우 끝부분 두개가 이벤트이다. 이벤트들을 x축으로 정렬한다. 인덱스 사이에서는 높이가 변하지 않는다. 따라서 높이를 구한뒤 다음 인덱스까지의 x값을 곱하면 쉽게 넓이를 구할 수 있다.)
(다각형 교집합의 넓이- 다각형들의 꼭지점과 변들의 교차점들이 이벤트이다. 이 이벤트들을 x좌표로 수직선을 그으면 이벤트 사이는 모두 사다리꼴형태가 되어 넓이를 쉽게 찾을 수 있다.)
(교차하는 선분들(샤모스-호이 알고리즘, 벤틀리-오트만 알고리즘)- 평면 위 선분들의 집합이 주어질 때 이들 중 서로 교차하는 것이 있는지 찾는 문제. 선분들의 왼쪽 끝 점과 오른쪽 끝 점이 이벤트이다. 스위핑하면서 선분의 왼쪽 끝점을 만나면 집합에 추가하고 오른쪽 끝점을 만나면 집합에서 뺀다. 이 집합은 항상 각 선분이 수직선을 만나는 y 좌표가 증가하는 순으로 정렬 해둔다. 새로운 선분이 추가되면 새 선분과 인접한 두 선분의 교차 여부를 확인한다. 선분이 삭제될 때마다 집합 상에서 이 선분과 인접해 있던 두선분의 교차 여부를 확인한다. 인접한 부분을 찾으면 함수를 종료한다.)
회전하는 캘리퍼스(Rotating Calipers)
캘리퍼스란 작은 물건의 지름, 너비등을 측정할 때 쓰는 공구로, 두 개의 평행한 변 사이에 물체를 끼우고 변 사이의 길이를 재는 도구이다.
(블록 다각형의 지름: 다각형을 평행한 두 직선 사이에 끼우고, 다각형을 따라 직선을 한 바퀴 돌리면서
직선에 닿는 꼭짓점들 간의 거리를 잰다. 가장 긴 거리가 지름이다.
가장 왼쪽과 오른쪽 점을 찾아낸 뒤, 각각에 두개의 수직선을 붙인다.
두 벡터는 방향이 항상 반대이기 때문에 한 방향벡터만 저장한다.
어느 쪽이 먼저 다각형의 다른 점을 만나는지를 계산한다.
이를 위해 현재 수직선의 방향과 다음 점까지의 방향 사이의 각도를 계산해야한다.
더 작은 각도쪽을 택해 두 직선을 회전한다.
회전하는 것은 직선의 방향을 갱신하고, 회전의 축이 되는 점을 다음 점으로 옮기는 방식이다.)
자주 하는 실수와 유의점들
퇴화 도형(degenerate)
일반위치(general position): 도형들의 상대적 위치의 일반적인 경우
퇴화 도형:
일직선 상에 있는 세개 이상의 점들,
서로 평행하거나 겹치는 직선/선분들,
넓이가 0인다각형들,
다각형들의 변들이 서로 겹치는 경우
항상 퇴화 도형들을 신경써서 문제를 고려해야한다.
직교 좌표계와 스크린 좌표계
직교좌표계, 데카르트 좌표계(Cartesian coordinate system):
y,x 좌표
스크린 좌표계:
배열상 원소의 위치, 컴퓨터 스크린의 픽셀 위치 (0이 맨위)
다른 실수들
많은 기하 문제들은 정수만을 사용해 해결할 수 있다
수치적 불안정하다고 느껴질 경우 정수나 분수 연산만을 통해 정확성 확보
acos asin atan2 함수들은 느리고 수치적으로 불안정하다.
acos asin 은 입력으로 -1 +1 범위의 실수만 받아들인다.
오차 가 더 크거나 작을 때-> NAN반환
-> acos(max(-1.0, min(1.0,x))) 범위 제한 필요
sqrt에 아주 작은 음수가 들어가는 실수
-> sqrt(max(0.0, x)) 범위 제한 필요
-알고리즘 문제해결전략 517p
'알고리즘 > 알고리즘 정리' 카테고리의 다른 글
| [선형 자료 구조] 동적 배열과 연결 리스트 (0) | 2021.01.29 |
|---|---|
| [부분 합] Partial sum (0) | 2021.01.28 |
| [정수론] [정리 필요]number theory (0) | 2021.01.23 |
| [수치 해석] Numerical analysis (0) | 2021.01.22 |
| [결정 문제] 최적화 문제를 결정문제로 바꿔 풀기 (0) | 2021.01.21 |