2021. 2. 11. 21:23ㆍ알고리즘/알고리즘 정리
1. 그래프 탐색 (search)
그래프의 모든 정점들을 특정한 순서에 따라 방문하는 알고리즘들을 그래프의 탐색이라고 한다
탐색 과정에서 어떤 간선이 사용되었는지, 또 어떤 순서로 정점들이 방문되었는지를 통해 그래프의 구조를 알 수 있다.
2. 깊이 우선 탐색 (Depth-first search, DFS)

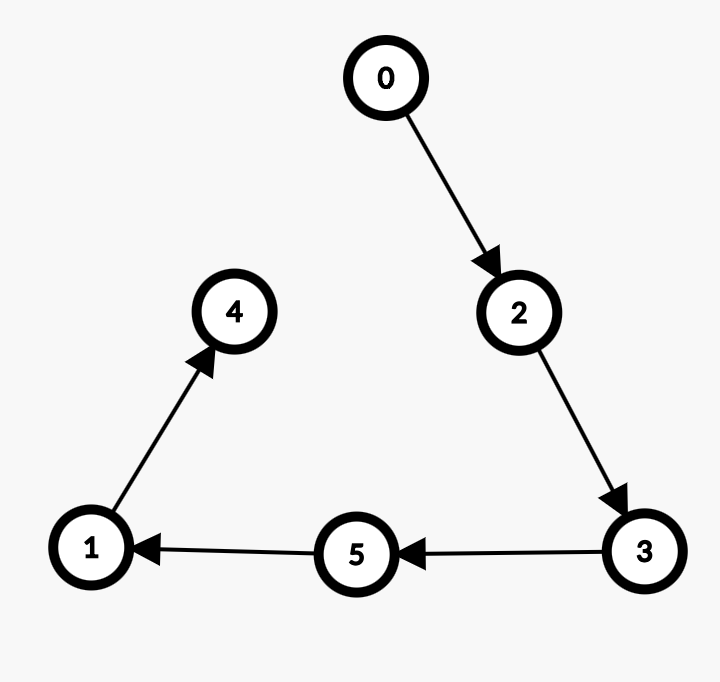


그래프의 모든 정점을 발견하는 가장 단순하고 고전적인 방법이다
현재 정점과 인접한 간선들을 하나씩 검사하다가, 아직 방문하지 않은 정점으로 향하는 간선이 있다면
그 간선을 무조건 따라가는 것 이다.
따라갈 간선이 없으면 마지막에 따라왔던 간선을 따라 뒤 돌아간다.
위 그림들은 정점의 번호가 작은것을 먼저 탐색하는 dfs의 예시이다.
깊이 우선 탐색의 중요한 특성은 더 따라갈 간선이 없을 경우 이전으로 돌아간다는 점이다.
이러한 특성때문에 재귀 호출을 이용하면 쉽게 구현 할 수 있다.
재귀 호출한 함수가 종료하면 호출한 위치로 다시 돌아가기 때문이다.
3. 깊이 우선탐색: 인접 리스트 표현 구현
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
|
vector<bool> visited;
void dfs(int here) {
cout<<"DFS visits "<< here <<endl;
visited[here] = true;
for(int i = 0 ; i < adj[here].size(); ++i) {
int there = adj[here][i];
if(!visited[there])
dfs(there);
}
}
void dfsAll() {
visited = vector<bool> (adj.size(), false);
for(int i = 0; i < adj.size(); i++) {
if(!visited[i])
dfs(i);
}
}
|
cs |
그래프에서는 모든 정점들이 간선을 통해 연결되어 있다는 보장이 없으므로
dfsAll 함수가 모든 정점들을 탐색할 수 있게 보장해준다.
DFS 예시들
두 정점이 서로 연결되어 있는지? dfs -> visited 참조
연결된 부분집합(컴포넌트)의 개수 세기- dfsall -> dfs실행횟수
4. 깊이 우선 탐색의 시간 복잡도
깊이 우선 탐색의 시간 복잡도는 어떤 표현 방식을 사용하느냐에 따라 달라진다.
dfs는 한 정점마다 한 번씩 호출되므로, 정확히 |V|번 호출된다.
dfs의 한 번의 수행 시간은 모든 인접 간선을 검사하는 for문에 의해 지배되는데,
인접 리스트로 표현할 경우
모든 정점에 대해 dfs를 수행하고 나면 모든 간선을 정확히 한번(방향) 혹은 두번(무향) 확인한다.
따라서 DFS 의 시간 복잡도는 O(|V| + |E|)가 된다.
인접 행렬로 표현할 경우
dfs의 호출횟수는 그대로 |V|번이고
for문이 |V| 번 모든 정점과 연결되어 있는지 검사하므로
총 시간 복잡도는 O(|V|^2)이 된다.
5. 위상정렬 (topological sort): 의존성 그래프 (dependency graph)

위상 정렬은 의존성이 있는 작업들이 주어질 때 이들을 어떤 순서로 수행해야 하는지 계산해준다.
작업 B를 하기 전에 반드시 작업 A를 해야 한다면,
작업 B가 작업 A에 의존한다고 한다.
각 작업을 정점으로 표현하고, 작업 간의 의존 관계를 간선으로 표현한
방향 그래프를 의존성 그래프라고 한다.
작업 v가 u에 의존한다면 의존성 그래프는 간선 (u,v)를 포함하게 된다.
의존성 그래프의 가장 큰 특성은 '사이클'이 없다는 점이다.
따라서 의존성 그래프는 사이클 없는 방향 그래프 DAG 가 된다.

의존성 그래프의 정점들을 일렬로 늘어놓고, 왼쪽에서부터 하나씩 수행한다고 할때
모든 의존성을 만족하는 경우는, 모든 간선이 왼쪽에서 오른쪽으로 가야한다.
이렇게 DAG의 정점을 배열하는 문제를 위상 정렬이라고 한다.
- 위상정렬을 구현하는 가장 직관적인 방법: 들어오는 간선이 하나도 없는 정점들을 하나씩 찾아서 정렬 결과의 뒤에 붙임.
- 그래프에서 이 정점을 지우는과정을 반복.
이는 깊이 우선 탐색을 이용하면 더 간단하게 구현할 수 있다.
dfsAll() 을 수행하며 dfs가 종료할 때마다 현재 정점의 번호를 기록하는 것.
(dfs함수가 재귀적으로 호출됨을 주의)
dfsAll()이 종료한 뒤 기록된 순서를 뒤집으면 위상 정렬 결과를 얻을 수 있다.
따라서 dfs가 늦게 종료한 정점일 수록 정렬 결과의 앞에 온다
6. 귀류법을 통한 dfs-> 위상정렬 증명
V-o-o-U
<-------
위상 정렬 결과에서 왼쪽에서 오른쪽으로 가는 간선(u, v)가 있다고 해보자
이것은 dfs(u)가 종료된 후 dfs(v)가 종료 되었다는 의미이다. (나중에 종료된게 앞에 있다)
하지만 dfs(u) 함수가 종료되기전 u와 이어지는 모든 정점을 들려 함수를 실행하고 종료시킨다.
그러므로 dfs(u)는 v또한 검사를 했을 것이다.
검사에서 visited가 다음과 같다고 해보자
visited[v] = true : v를 이전에 검사했다. 하지만 앞에있다. 그러므로 u 보다 나중에 종료 되었다.
하지만 u에서 v를 검사했다. 이는 '사이클'이 생긴것이므로 위상 정렬이 불가능하다.
visited[v] = false: v가 이전에 안나왔다. 하지만 u보다 나중에 종료되었다. 그런데 u에서 v를 가게 되면
v가 먼저 종료되어야한다. 이는 모순적이다.
검사 결과가 모순적이기 때문에 오른쪽에서 왼쪽으로 가는 간선은 존재할 수 없으며, 이를 통해
검사하는 그래프가 DAG이면 항상 DFS로 위상정렬을 만들 수 있음을 알 수 있다.
- 알고리즘 문제해결전략 825p
'알고리즘 > 알고리즘 정리' 카테고리의 다른 글
| [그래프] Graph 4: DFS의 응용: 간선 분류-dfs 스패닝 트리, 절단점, 강결합 컴포넌트 분리 (2) | 2021.02.14 |
|---|---|
| [그래프] Graph 3: Eulerian circuit 오일러 서킷, 오일러 트레일 (0) | 2021.02.13 |
| [그래프] Graph 1: 그래프의 표현과 정의 (0) | 2021.02.11 |
| [트리] Tree 9: 트라이, 아호-코라식 알고리즘 (0) | 2021.02.09 |
| [트리] Tree 8: Disjoint Set 상호 배타적 집합, 유니온-파인드 (0) | 2021.02.08 |