2021. 2. 22. 19:40ㆍ알고리즘/알고리즘 정리
1. 최소 스패닝 트리(Minimum Spanning Tree)
외판원 문제 휴리스틱에서나 각종 그래프의 탐색 알고리즘, 최단 경로 알고리즘에서 경로를 찾는데에 사용했었다.
어떤 무향 그래프의 스패닝 트리(Spanning Tree)는 원래 그래프의 정점 전부와 간선의 부분 집합으로 구성된 부분 그래프이다.
이때 스패닝 트리에 포함된 간선들은 정점들을 트리 형태로 전부 연결해야한다.
트리 형태라는 것은 선택된 간선들이 사이클을 이루지 않는다는 것을 의미하며,
정점들이 꼭 부모-자식 관계로 연결될 필요는 없다는 것을 의미한다.
또한 그래프안에 여러 개의 스패닝 트리가 있다.
이런 스패닝 트리 중에서 가중치의 그래프의 스패닝 트리 중 가중치 합이 가장 작은 트리를 찾는 문제를
최소 스패닝 트리 문제(Minimum Spanning Tree)라고 한다.
2. 두 가지 알고리즘: 크루 스칼 알고리즘, 프림 알고리즘
크루스칼 알고리즘은 상호 배타적 집합 자료 구조의 좋은 사용 예이다.
프림 알고리즘은 다익스트라 알고리즘과 거의 같은 형태를 띠고 있다.
이 두 알고리즘은 접근 방법이 아주 다르지만 결국 같은 방법으로 증명할 수 있다.
두 알고리즘은 모두 간선이 하나도 없는 상태에서 시작해 하나씩 트리에 간선을 추가해 가는 탐욕적 알고리즘으로
본질적으로 같은 방법으로 증명할 수 있다.
3. 크루스칼의 최소 스패닝 트리 알고리즘
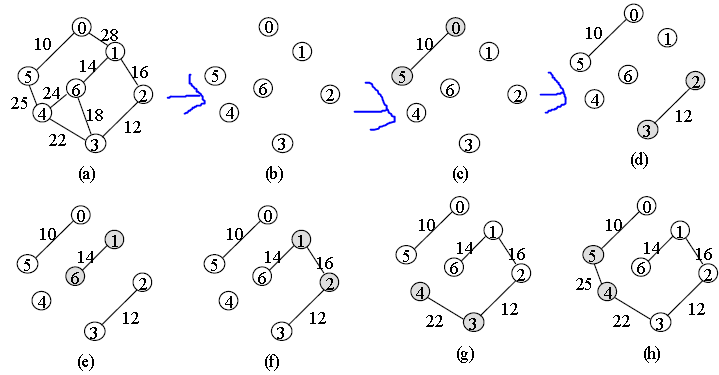
그래프의 모든 간선을 가중치의 오름차순으로 정렬한 뒤,
스패닝 트리에 하나씩 추가한다.
이때 사이클이 생기는 간선은 제외한다.
모든 간선을 한 번씩 검사하고 난 뒤 종료한다.
자료 구조의 선택
간선을 트리에 추가했을 때 이미 추가한 간선들과 합쳐 사이클을 이루는지 여부를 판단하는 부분이 핵심이다.
이 작업을 효율적으로 수행하기위해 적절한 자료구조를 선택해야한다.
1. 트리에 dfs를 수행하며 역방향 간선이 있는지 확인한다.
각 간선마다 한 번씩 조사하기 때문에 전체 시간 복잡도는 O(|E|^2) 이 된다.
2. 어떤 간선을 추가해서 그래프에 사이클이 생기려면 간선의 양 끝 점은 같은 컴포넌트에 속해있어야한다.
그러므로 상호 배타적 집합 자료구조를 사용하면 두 정점이 이미 같은 집합에 속해 있는지를 확인하고
간선을 트리에 추가할 경우 두 집합을 합치는 연산을 빠르게 할 수 있다. O(ElgE)
구현
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
|
struct DisjointSet{
vector<int> father, rank;
DisjointSet(int V) : father(V, 0) , rank(V, 1)
{
for(int i = 0; i < V; i++)
father[i] = i;
}
int find(int u)
{
if(father[u] == u) return u;
return father[u] = find(father[u]);
}
void merge(int u, int v)
{
u = find(u); v = find(v);
if(u == v) return;
if(rank[u] > rank[v]) swap(u, v);
father[u] = v;
if(rank[u] == rank[v]) rank[v]++;
}
};
const int MAX_V = 100;
int V;
vector<pair<int, int> > adj[MAX_V];
int kruskal(vector<pair<int, int> >& selected)
{
int ret = 0;
selected.clear();
vector<pair<int, pair<int, int> > > edges;
for(int u = 0; u < V; ++u)
for(int i = 0; i < adj[u].size(); ++i)
{
int v = adj[u][i].first, cost = adj[u][i].second;
edges.push_back(make_pair(cost, make_pair(u, v)));
}
sort(edges.begin(), edges.end());
DisjointSet sets(V);
for(int i = 0; i < edges.size(); i++)
{
int cost = edges[i].first;
int u = edges[i].second.first, v = edges[i].second.second;
if(sets.find(u) == sets.find(v)) continue;
sets.merge(u, v);
selected.push_back(make_pair(u, v));
ret += cost;
}
return ret;
}
|
cs |
정당성의 증명
뒤에 오는 간선들에 대한 고려는 하지 않으므로 탐욕적 알고리즘으로 분류할 수 있다.
그래서 크루스칼 알고리즘의 정당성 증명은 일반적인 탐욕법 알고리즘과 같은 형태로 할 수 있다.
1. 탐욕적 속성
탐욕적인 선택으로 인해 손해를 볼 일이 없음을 증명
= 어떤 간선을 추가하기로 결정했을 때 이로 인해 MST를 찾을 수 없게되는 일이 없다는 점을 증명
2. 최적 부분 조건
= 항상 최적의 선택만 내려도 전체 문제의 최적해를 얻을 수 있음을 보인다.
귀류법:
크루스칼 알고리즘이 선택하는 간선 중 그래프의 최소 스패닝 트리 T에 포함되지 않는 간선이 있다고 하자.
이 중 첫 번째로 선택되는 간선을 (u,v)라 하자.
T는 이 간선을 포함하지 않으니, u와 v는 T상에서 다른 경로로 연결되어 있다.
주목할 것은 이 경로를 이루는 간선 중 하나는 반드시 (u, v)와 가중치가 같거나 커야만 한다.
이 간선들이 모두 (u, v)보다 가중치가 작다면 크루스칼 알고리즘이
이미 이 간선들을 모두 선택해서 u 와 v를 연결했을 것이므로 (u, v)를 선택될 일 이 없었을 것이다.
따라서 이 경로 상에서 (u, v)이상의 가중치를 갖는 간선 하나를 골라 T에서 지워버리고 (u, v)를 추가하면
이 결과도 여전히 스패닝 트리이며, 가중치의 총합은 줄어도 늘지는 않는다.
T가 이미 MST라고 가정했으므로, 이 변경을 거친 결과 또한 MST이다
따라서 (u, v)를 선택한다고 해도 남은 간선들을 잘 선택하면 항상 최소 스패닝 트리를 얻을 수 있다.
이 속성은 마지막 간선을 추가해서 스패닝 트리가 완성될때까지 성립하며
마지막에 얻은 트리는 항상 MST가 된다.
4. 프림 알고리즘

프림 알고리즘과 크루스칼 알고리즘의 큰 차이는 진행 방식이다.
크루스칼 알고리즘에서는 여기저기서 산발적으로 만들어진 트리의 조각들을 합쳐 스패닝 트리를 만드는 반면
프림 알고리즘에서는 하나의 시작점으로 구성된 트리에 간선을 하나씩 추가하며 스패닝 트리가 될 때까지 키워간다
따라서 항상 선택된 간선들은 중간 과정에서도 항상 연결된 트리를 이루게 된다.
이미 만들어진 트리에 인접한 간선만을 고려한다는 점만 빼면 크루스칼 알고리즘과 완전히 똑같다.
선택할 수 있는 간선들 중 가중치가 가장 작은 간선을 선택하는 과정을 반복하기 때문이다.
구현
포함되었는지 확인하기위해 불린 값 배열 added[]를 생성한다.
각 차례마다 모든 간선을 순회하면서 다음으로 추가할 간선을 찾으면 시간 복잡도는 O(VE)가 된다.
이는 한 정점에 닿는 간선이 두 개 이상일 경우 이들을 하나하나 검사하지 않으므로써 최적화 시킬 수 있다.
각 정점에 대해 트리와 이 정점을 연결하는 가장 짧은 간선에 대한 정보를 저장하는 것이다.(O(V^2)
따라서 이러한 간선의 최소 가중치를 저장하는 배열 minWeight[]를 유지한다
이 배열은 트리에 정점을 새로 추가할 때마다 이 정점에 인접한 간선들을 순회하면서 갱신하게 되는것이다.
이렇게 하면 추가할 새 정점을 찾는 작업은 O(|V|)만에 할 수 있고, 모든 간선은 두 번씩만 검사되므로 전체 시간복잡도는 O(V^2 + E) 가 된다, 거의 모든 정점들 사이에 간선이 있는 밀집 그래프의 경우 E ≒ V^2 이므로 프림 알고리즘은 이 경우 크루스칼 보다 빠르게 동작한다.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
|
const int MAX_V =100;
const int INF = 987654321;
int V;
vector<pair<int , int> > adj[MAX_V];
int prim(vector<pair<int, int> >& selected)
{
selected.clear();
vector<bool> added(V, false);
vector<int> minWeight(V, INF), parent(V, -1);
int ret = 0;
minWeight[0] = parent[0] = 0;
for(int iter = 0; iter < V; ++iter)
{
int u = -1;
for(int v = 0; v < V; ++v)
if(!added[v] && (u == -1 || minWeight[u] > minWeight[v]))
u = v;
if(parent[u] != u)
selected.push_back(make_pair(parent[u], u));
ret += minWeight[u];
added[u] = true;
for(int i = 0; i < adj[u].size(); i++)
{
int v = adj[u][i].first, weight = adj[u][i].second;
if(!added[v]&& minWeight[v] > weight)
{
parent[v] = u;
minWeight[v] = weight;
}
}
}
return ret;
}
|
cs |
다른 구현
위 코드는 우선 순위 큐를 사용하지 않고 다익스트라 알고리즘을 구현한 것과 비슷하다
따라서 우선순위 큐를 사용하면 O(ElgV) 시간복잡도를 가지는 프림 알고리즘을 구현할 수 있다.
이 경우 우선순위 큐는 각 정점의 번호를 minWeight[]이 증가하는 순으로 정렬해 담고 있게 된다
정당성의 증명
프림 알고리즘은 매 반복마다 지금 만들어진 트리에 인접한 간선들만을 고려한다는 점을 제외하고는 크루스칼 알고리즘과 똑같다.
따라서 증명또한 똑같다
선택한 간선 (u,v)를 포함하지 않는 MST에서
u와 v를 잇는 경로 위의 모든 간선이 (u, v)보다 가중치가 작을 일은 없다는 점은
프림알고리즘에서도 그대로 성립한다,
- 알고리즘 문제해결전략 969p
'알고리즘 > 알고리즘 정리' 카테고리의 다른 글
| [그래프] Graph 12: 네트워크 모델링(Network flow): 예제를 통한 그래프 표현 (0) | 2021.02.24 |
|---|---|
| [그래프] Graph 11: 네트워크 유량(Network flow) : 포드-풀커슨 알고리즘 (0) | 2021.02.23 |
| [그래프] Graph 9: Floyd 플로이드의 모든 쌍 최단 거리 알고리즘 (0) | 2021.02.20 |
| [그래프] Graph 8: 벨만-포드 최단 경로 알고리즘 (0) | 2021.02.19 |
| [그래프] Graph7 : 다익스트라 : 최단 경로 알고리즘: 가중치 있는 그래프 (0) | 2021.02.18 |