2021. 6. 26. 14:18ㆍ알고리즘/알고리즘 정리
1. 11050
파스칼 삼각형을 사용해 문제를 해결 하였다.

|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
|
#include <iostream>
using namespace std;
int cache[11][12];
void initial() {
for(int i = 0; i <= 10; i++) {
cache[i][0] = 1; cache[i][i+1] = 0;
for(int j = 1; j <= i; j++) {
cache[i][j] = cache[i-1][j-1] + cache[i-1][j];
}
}
}
int main() {
int N, K;
cin>>N>>K;
initial();
cout<<cache[N][K];
}
|
cs |
2. 11051
위 문제의 변형
10007로 나눈 결과값을 리턴하는 문제
모듈라 연산의 성질을 사용하여 나머지만 저장하였다.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
|
#include <iostream>
using namespace std;
int cache[1001][1002];
void initial() {
for(int i = 0; i <= 1000; i++) {
cache[i][0] = 1; cache[i][i+1] = 0;
for(int j = 1; j <= i; j++) {
cache[i][j] = (cache[i-1][j-1] + cache[i-1][j])%10007;
}
}
}
int main() {
int N, K;
cin>>N>>K;
initial();
cout<<cache[N][K];
}
|
cs |
3. 11401 => 페르마 소정리, 확장 유클리드
3.1 페르마의 소정리
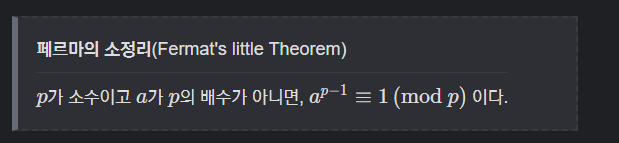
기존의 이항계수의 식은 다음과 같다
nCk = n! / (k! * (n-k)!)
이식에서 p로 나눈 나머지는
nCk % p = n! % p / (k! * (n-k)!) %p
이런 식으로 구할 수 없다.
모듈라연산에서 나눗셈의 나머지는
나누는 대신 곱셈의 역원과의 곱으로 표현하여 연산을한다.
이러한 곱셈의 역원은 페르마의 소정리를 통하여 구할 수 있다.
위의 합동식에서 a를 나누는 것
| *항등원과 역원 (항등원 => 임의의 원소a와 임의의 연산?에 대해 a?x = a 이 되게하는 x ) (역원 => 임의의 원소 a와 임의의 연산 ?에 대해 a?x = 0 이 되게하는 x ) 어떤 수를 a로 나눈다 == 어떤 수를 a의 곱셈에 대한 역원과 곱한다 => 만약 a의 곱셈에 대한 역원이 존재하지 않으면.... 나눗셈 정의 하지 못함 *합동식에서 곱셈의 역원이 존재할 조건 gcd(a, p) = 1 p와 a 가 서로소이면 법 p에 대해 a의 역원이 존재한다 = p와 a 가 서로소인 경우, 법 p의 합동식에서 양변을 a로 나눌 수 있다 => p가 소수일때, 법 p의 합동식에서는 양변을 p의 배수가 아닌 임의의 수로 나눌 수 있다. 정수론 (4) - 합동식에서의 나눗셈 (tistory.com) |
a로 나누면 다음과 같은 식이 나온다.
a^(p-2) ≡ a^-1 mod p
a 를 (k! * (n-k)!) 라고 두면 다음과 같은 식이 성립하게된다.
nCk % p = n! % p * (k! * (n-k)!)^(p-2)%p
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
|
#include <iostream>
using namespace std;
long long N, K;
long long p = 1000000007;
long long fact(long long n) {
if(n <= 1) return 1;
return (fact(n-1)*n)%p;
}
long long powll(long long n, long long k) {
if(k == 1) {
return n;
}
if(k%2 == 0) {
long long t = powll(n, k/2);
return (t*t)%p;
}
else {
return (powll(n, k-1)*n)%p;
}
}
long long solve(long long n, long long k) {
return (fact(n) * powll((fact(k)*fact(n-k))%p, p-2))%p;
}
int main() {
cin>>N>>K;
cout<<solve(N, K);
}
|
cs |
3.2 확장 유클리드
| 베주항등식 : 적어도 둘 중 하나는 0이 아닌 정수 a, b가 있을 때 다음 세 명제가 성립한다. 1. gcd(a, b) = ax + by 를 성립하게 만드는 정수 x, y가 반드시 존재한다. 2. gcd(a, b) 는 정수 x, y에 대하여 ax + by 형태로 표현할 수 있는 가장 작은 자연수이다. 3. 정수 x, y에 대하여 ax + by 형태로 표현되는 모든 정수는 gcd(a, b)의 배수이다. => 베주 항등식은 x, y의 존재성에대해서만, 확장 유클리드 알고리즘을 통해 x, y를 구할 수 있다. |
확장 유클리드 알고리즘 : 유클리드 알고리즘을 거꾸로한것
1. 유클리드 호제법을 통해 a, b의 최대공약수를 구함
2. 유클리드 호제법의 식들을 위에서부터 1, 2, ... ,n번 식이라고 했을 때, 먼저 n - 1번 식을 나머징 대해 이항
3. n-2번 식을 나머지에 대해 이항한뒤, n-1번 식에 대입
4. n-3번 식을 나머지에 대해 이항한뒤, n-1번 식에 대입
5. gcd(a, b) = ax + by 의 꼴로 표현될 때 까지 반복
문제에서 풀어야하는 조합식 분수부분을 a라 하고 나눠야하는 수를 p라고 하자
p가 소수로 주어졌으니 gcd(a, p) = ax + py = 1
ax ≡ 1 mod p
x ≡ a^-1 mod p
즉, x를 구할 수 있으면 nCk % p = n! % p * (x)%p 이 식을 통해 답을 구할 수 있다.
| 주의점 - 확장 유클리드 호제법은 구하려는 값 X가 음수가 나올 수 있다. 따라서 (x + p)%p를 해줘서 양수로 만들어줘야한다. |
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
|
#include <iostream>
using namespace std;
long long N, K;
long long p = 1000000007;
long long fact(long long n) {
long long ret = 1;
for(int i = 2; i <= n; i++) {
ret = (i*ret)%p;
}
return ret;
}
//gcd(a, b) = bx + ay
// b * xy.first + a * xy.second
long long gcd(long long a, long long b, pair<long long, long long>& xy) {
if(a == 0) {
xy.first = 0;
xy.second = b;
return b;
}
int ret = gcd(b % a, a, xy);
if(b % a != 0) {
long long f = xy.first;
xy.first = xy.second;
xy.second = xy.second * (-b / a) + f;
}
return ret;
}
long long solve1(long long n, long long k) {
pair<long long, long long> xy;
long long x = gcd(fact(n - k) * fact(k), p, xy);
return (fact(n) * (xy.second + p)%p)% p;
}
int main() {
cin>>N>>K;
cout<<solve1(N, K);
}
|
cs |
4. 11402
11402번: 이항 계수 4
첫째 줄에 \(N\), \(K\)와 \(M\)이 주어진다. (1 ≤ \(N\) ≤ 1018, 0 ≤ \(K\) ≤ \(N\), 2 ≤ \(M\) ≤ 2,000, M은 소수)
www.acmicpc.net
뤼카의 정리를 통해 빠르게 이항계수를 구할 수 있다
이 정리는 간단하게 정리하겠다.
이 정리는 소수 p 로 나눈 나머지를 구하는게 목적이다
n과 k를 p진법으로 풀어서 각각 차수에 맞게 끔 이항계수를 만든 다음(nCk)
이들을 곱하고 p로 나눈 값이 우리의 목적의 값과 똑같다는 내용이다.
(단 이때 k가 n보다 큰 경우 무조건 나머지는 0)
식으로 간략하게 표현한것은 다음과 같다
nCk % p = (n_0Ck_0 * n_1Ck_1 * ... n_jCk_j ) % p
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
|
nclude <iostream>
#include <algorithm>
#include <vector>
using namespace std;
long long cache[2002][2002];
void initial(long long M) {
for(int i = 0; i < 2001; i++) {
cache[i][i+1] = 0; cache[i][0] = 1;
for(int j = 1; j <= i; j++) {
cache[i][j] = (cache[i-1][j] + cache[i-1][j-1])%M;
}
}
}
vector<long long> decimalToM(long long N, long long M) {
vector<long long> ret;
do {
ret.push_back(N%M);
N/= M;
}while(N!= 0);
return ret;
}
long long sol(long long N, long long K, long long M) {
vector<long long> nlist = decimalToM(N, M);
vector<long long> klist = decimalToM(K, M);
long long ret = 1;
for(int i = 0; i < nlist.size(); i++) {
if(klist.size() <= i) {
break;
}
if(nlist[i] < klist[i]) {
return 0;
}
ret = (ret * cache[nlist[i]][klist[i]])%M;
}
return ret;
}
// N <= 1e18 , M <= 2000
int main() {
long long N, K, M;
cin>>N>>K>>M;
initial(M);
cout<<sol(N, K, M);
}
|
cs |
'알고리즘 > 알고리즘 정리' 카테고리의 다른 글
| [그래프] Graph 13: maximum matching 이분 그래프에서 최대 매칭 (0) | 2021.02.25 |
|---|---|
| [그래프] Graph 12: 네트워크 모델링(Network flow): 예제를 통한 그래프 표현 (0) | 2021.02.24 |
| [그래프] Graph 11: 네트워크 유량(Network flow) : 포드-풀커슨 알고리즘 (0) | 2021.02.23 |
| [그래프] Graph 10: 최소 스패닝 트리: 크루스칼, 프림 알고리즘 (0) | 2021.02.22 |
| [그래프] Graph 9: Floyd 플로이드의 모든 쌍 최단 거리 알고리즘 (0) | 2021.02.20 |