2021. 2. 25. 17:31ㆍ알고리즘/알고리즘 정리
1. 매칭 문제
N명을 둘씩 짝으로 묶으려고한다.
단 사이가 좋은 사람끼리만 짝을 지어준다고 할때
모든 학생에게 짝을 지어 줄 수 있는지, 불가능하다면 최대 몇 쌍이나 만들 수 있는지 계산하는 문제가
매칭 문제의 예시이다.
이런 문제들은 그래프로 간단하게 표현할 수 있다.
각 사람을 표현하는 정점을 만든 뒤, 사이 좋은 학생들을 간선으로 연결한다.
이 때 서로 짝을 이룬 학생들을 연결하는 간선들을 모아 보면, 이들은 끝점을 공유하지 않는 간선의 집합이 된다.
이런 간선의 집합을 이 그래프의 매칭(matching)이라고 한다.
이때 가장 큰 매칭을 찾아내는 문제를 최대 매칭 문제(maximum matching), 매칭 문제라고 부른다.
매칭 문제는 직관적인 정의를 가진 중요한 문제이다.
하지만 모든 그래프에 대해 매칭 문제를 해결하는 일반적인 알고리즘은 꽤나 복잡하고 까다롭다.
프로그래밍 대회에서는 매칭의 좀더 단순한 형태가 등장한다.
이분 그래프에서 최대 매칭을 찾는 문제가 주로 나온다고 한다.
2. 이분 매칭의 중요성
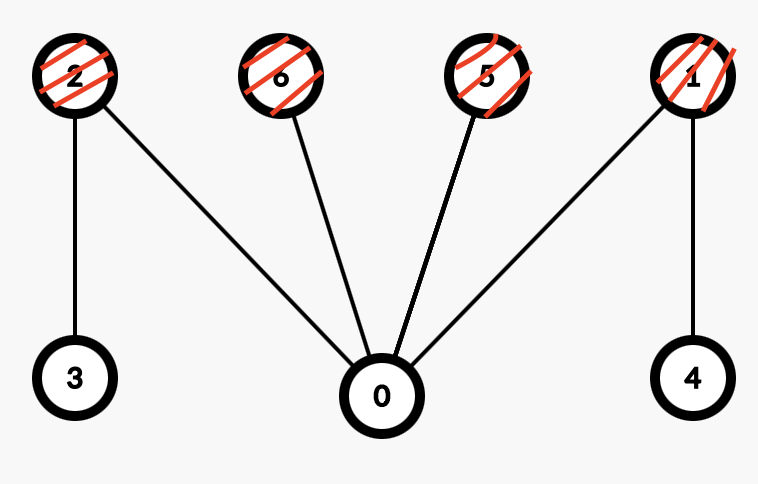
모든 간선이 서로 다른 그룹의 정점들을 연결하도록 할 수 있는 그래프들을 이분 그래프라고 한다.
정점의 집합을 색으로 구분해보면, 모든 간선이 서로 다른 색의 정점을 연결하고 있는것을 볼 수 있다.
이분 그래프는 두 집합 간의 대응 관계를 표현하기 위해 흔히 사용된다.
가장 전형적인 예로 작업 배분을 들 수 있다.
모든 사람이 다 모든 작업을 할 수 있는 것은 아니라고 하자,
이와 같은 제약 조건을 이분 그래프로 쉽게 표현할 수 있다.
각 사람을 나타내는 정점과 작업을 나타내는 정점들을 갖는 그래프를 만든 뒤,
각 사람과 그 사람이 할 수 있는 작업을 간선으로 연결하면 된다.
이와 같은 이분 그래프에서 최대 매칭은 가능한 한 많은 작업과 사람을 짝지을 수 있는 방법을 나타낸다.
이렇게 이분 그래프는 현실 세계에서 직관적인 의미를 가지기 때문에 이분 그래프에 대한 매칭은 따로 언급할 가치가 있다.
3. 네트워크 유량으로 이분 매칭 풀기
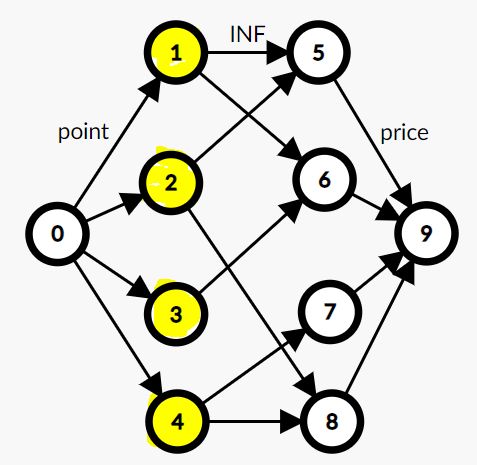
네트워크 유량을 이용하면 이분 매칭을 아주 간단하게 풀 수 있다.
그룹을 나누어 위와 같이 소스와 싱크를 붙이면 된다.
이때 모든 간선의 용량을 1 로 하고 이 그래프의 최대 유량을 구한 뒤 유량이 흐르는 간선들을 모으면 최대 매칭이 됨을 알 수 있다.
이 경우 네트워크의 최대 유량이 O(|V|)이므로 bfs는 최대 O(|V|)번만 하게 된다. 따라서 시간 복잡도는 O(|E||V|)가 된다.
4. 이분 매칭 구현하기
포드-풀커슨 알고리즘을 응용해서 이분 매칭을 구현할 수도 있지만,
이분 매칭 문제는 일반적인 네트워크 유량 문제보다 비교적 자주 출현하기 때문에
좀더 단순한 형태의 코드를 작성하는게 편리하다.
이분 매칭의 속성을 이용하면 단순한 알고리즘을 구현할 수 있다.
이 구현은 포드-풀커슨 알고리즘처럼 증가 경로를 찾은 뒤 유량을 보내는 것을 반복한다
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
|
const int MAX_N = 100, MAX_M = 100;
int n, m;
bool adj[MAX_N][MAX_M];
vector<int> aMatch, bMatch;
vector<bool> visited;
bool dfs(int a)
{
if(visited[a]) return false;
visited[a] = true;
for(int b = 0; b < m; b++)
if(adj[a][b])
if(bMatch[b] == -1 || dfs(bMatch[b]))
{
aMatch[a] = b;
bMatch[b] = a;
return true;
}
return false;
}
int bipartiteMatch()
{
aMatch = vector<int>(n, -1);
bMatch = vector<int>(m, -1);
int size = 0;
for(int start = 0; start < n; start++)
{
visited = vector<bool>(n, false);
if(dfs(start))
++size;
}
return size;
}
|
cs |
위 코드가 이용하는 첫 번째 속성은 이분 매칭을 푸는 유량 네트워크에서
최대 유량은 O(|V|)로 정해져 있다는 것이다.
포드-풀커슨 알고리즘을 DFS로 구현할 때 큰 문제는 수행시간이 총 유량에 비례한다는 점이다.
하지만 이렇게 최대 유량이 제한되어 있는 경우, DFS를 사용해도 문제가 없다.
코드에서 DFS는 증가 경로를 찾아냈는지 여부를 반환하는데, 참이 반환되었을 경우
해당 간선을 따라 유량을 보내기만 하면 된다.
이것으로 탐색 스패닝 트리상에서 각 정점을 조상하고 소스로부터 싱크까지의 경로를 찾는 작업을 생략할 수 있다.
모든 간선의 용량이 1 이기 때문에 모든 증가 경로의 용량이 1이라는점도 도움이 된다.
또 다른 속성은 증가 경로를 찾기 위해 탐색을 하는 도중 B에 포함된 정점에 도착했는데, 이 정점이 이미 매칭된 상황이라면
이 간선에 잔여 용량은 남아 있지 않을 것이다. 따라서 현재 정점으로 흘러오는 유량을 상쇄할 수 밖에 없는데, 현재 정점으로 유량을 보내 주는 정점은 현재 정점과 매칭된 정점밖에 없다.
dfs에서 a에 인접한 정점 b에 대해 b가 이미 매칭된 상태라면 b에 인접한 정점들을 순회하는 대신 b에 매칭된 정점 bmatch[b]로 곧장 재귀호출을 하는 부분은 이 속성을 이용한 것이다.
5. 더 공부할거리
- 디닉 알고리즘(포드-풀커슨 과 구조가 비슷하지만 한번에 가능한 많은 유량을 보내는 방식)
- 최대 유량 알고리즘의 변형인 최소 비용 최대 유량 (min cost max flow, MCMF)
최대 유량을 찾는데, 네트워크의 각 간선마다 유량을 1 흘려보낼 때 드는 비용이 정해져 있다고 하자
이때 최대 유량을 어떻게 흘려 보내야 비용의 합을 최소화할 수 있을지 계산하는 문제이다.
연속 최단 경로(successive shortest path) 알고리즘이 이에 해당한다
- 배정 문제 (assignment problem) 이분 매칭문제의 변형으로,
두 정점을 서로 연결하는 데 일정한 비용이 들 때 모든 정점을 서로 연결하기 위한 최소 비용을 찾아내는 문제이다.
최소 비용 최대 유량 알고리즘을 사용하여 쉽게 해결할 수 있지만
헝가리안 알고리즘(Hungarian algorithm)이라고 부르는 쿤-뭉크레스 알고리즘으로 풀 수 있다.
- 정점 덮개 문제 = 이분 그래프에 대해 쉽게 풀 수 있는 문제
그래프에서 정점의 부분 집합을 택했을 때 모든 간선에 대해 두 끝점 중 최소 하나는 이 집합에 포함된다면
이 부분 집합을 정점 덮개(vertex cover)라고 부른다. 직관적이지는 않지만,
이분 그래프에서 최소 정점 덮개의 크기는 최대 매칭의 크기와 같다는 사실이 증명되어 있다.
이는 콰닉의 정리라고 부른다.
- 네트워크 유량 알고리즘과 응용 문제의 바이블 : Network Flow(Ahuja, Magnanti, Orlin, 1993)
- 알고리즘 문제해결전략 1036p
'알고리즘 > 알고리즘 정리' 카테고리의 다른 글
| [백준][C++] 이항계수 구하기 1~4 (정수론- 페르마 소정리, 확장 유클리드, 뤼카의 정리) (0) | 2021.06.26 |
|---|---|
| [그래프] Graph 12: 네트워크 모델링(Network flow): 예제를 통한 그래프 표현 (0) | 2021.02.24 |
| [그래프] Graph 11: 네트워크 유량(Network flow) : 포드-풀커슨 알고리즘 (0) | 2021.02.23 |
| [그래프] Graph 10: 최소 스패닝 트리: 크루스칼, 프림 알고리즘 (0) | 2021.02.22 |
| [그래프] Graph 9: Floyd 플로이드의 모든 쌍 최단 거리 알고리즘 (0) | 2021.02.20 |